 Uno de los problemas clásicos de los sistemas de representación consiste en encontrar la intersección de dos elementos, como por ejemplo determinar el punto de intersección entre una recta y un plano. Son problemas de naturaleza topológica en los que priman los conceptos de pertenencia.
Uno de los problemas clásicos de los sistemas de representación consiste en encontrar la intersección de dos elementos, como por ejemplo determinar el punto de intersección entre una recta y un plano. Son problemas de naturaleza topológica en los que priman los conceptos de pertenencia.
Los problemas que se basan en relaciones topológicas son independientes del tipo de proyección en que se encuentren.
Los problemas de intersección se basan en determinar los elementos geométricos que pertenecen simultáneamente a dos elementos, considerando que éstos se encuentran formados por infinitos puntos.
Nos plantearemos como ejemplo de estudio el siguiente problema:
Hallar todos los puntos de intersección de la recta r con el prisma dado en perspectiva caballera, indicando la visibilidad de la recta. Para resolver este problema recordaremos previamente dentro de los problemas de incidencia, el de determinación del punto de intersección entre una recta y un plano.
 Hemos visto el modelo general para determinar las intersecciones en los sistemas de representación. En este planteamiento haremos pasar un plano auxiliar que contenga a la recta dada y que nos producirá una recta intersección con el plano.
Hemos visto el modelo general para determinar las intersecciones en los sistemas de representación. En este planteamiento haremos pasar un plano auxiliar que contenga a la recta dada y que nos producirá una recta intersección con el plano.
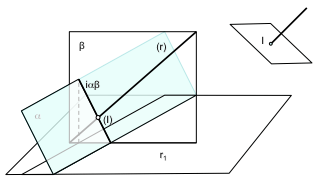
En este tipo de problemas, cuando la intersección sea con un prisma, deberemos repetir sistemáticamente el problema de intersección entre planos. Por ejemplo podemos resolver en primera instancia la intersección de una recta r con un ortoedro (una caja con caras paralelas y perpendiculares entre sí). La recta vendrá determinada por su proyección directa (r) y la proyección sobre el plano de la base (r1)
Para ello determinaremos un plano que contenga a la recta que, en este caso, sea ortogonal a la base. Este plano producirá unas rectas de intersección con el cuerpo que contendrán a los puntos de intersección.
- La determinación de estas rectas intersección se basará en las condiciones de paralelismo entre los diferentes planos del cuerpo, ya que un plano secciona a dos planos paralelos según rectas paralelas.
- Si el plano es perpendicular a la base, la intersección con otros planos perpendiculares a ésta determinará rectas verticales.
Si el cuerpo es más complejo deberemos resolver las intersecciones con algo más de trabajo, aunque el modelo general será el mismo si las caras siguen siendo paralelas a las de proyección.
Para la resolución de este ejercicio, se determina primero la sección que origina el plano que contiene a la recta r y a su proyección sobre el plano horizontal XY (r1), sobre el cuerpo prismático dado. Los puntos de entrada y salida (1, 2, 3, 4, 5 y 6) se obtienen como los puntos de intersección de la recta r con dicha sección.

Veremos más adelante cómo resolver casos en los que tengamos caras oblicuas.





Debe estar conectado para enviar un comentario.