 La utilización de las leyes de la dualidad en los modelos proyectivos nos permite obtener un conjunto de propiedades y teoremas duales a partir de otros previamente deducidos. La obtención de elementos homólogos en el caso de series proyectivas se realizaba obteniendo pespectividades intermedias mediante haces perspectivos que nos permitian obtener lo que hemos denominado “eje proyectivo”. Veremos que en el caso de haces proyectivos, el razonamiento dual nos lleva a determinar centros proyectivos.
La utilización de las leyes de la dualidad en los modelos proyectivos nos permite obtener un conjunto de propiedades y teoremas duales a partir de otros previamente deducidos. La obtención de elementos homólogos en el caso de series proyectivas se realizaba obteniendo pespectividades intermedias mediante haces perspectivos que nos permitian obtener lo que hemos denominado “eje proyectivo”. Veremos que en el caso de haces proyectivos, el razonamiento dual nos lleva a determinar centros proyectivos.
El “mundo” de los puntos es más asequible didácticamente que el dual de las rectas, por lo que hemos iniciado el análisis con los conceptos asociados a las series rectilineas para, ahora, realizar el mismo desarrollo en las formas duales, haces de rectas.
Podemos plantearnos en este estudio una serie de interrogantes básicos que servirán para guiar el desarrollo:
- ¿Cómo podemos definir dos haces proyectivos?
- ¿Cuántos elementos homólogos son necesarios para determinar una proyectividad
- ¿Cómo podemos obtener elementos homólogos de otros dados?
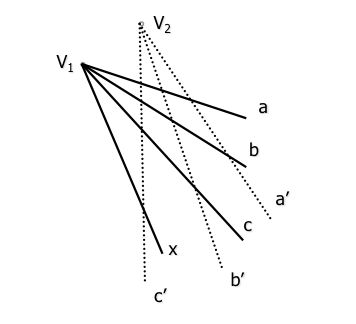
Dos haces proyectivos quedan determinados al definir tres parejas de rectas homólogas (a-a’, b-b’, c-c’), situados sobre sus respectivas bases (con origen en sus respectivos vértices).
A un cuarto elemento x del haz de vértice “V1” le corresponderá un nuevo rayo x’ del haz homólogo (proyectivo) de base (vértice) “V1”” de forma que se conserve la razón doble de las cuaternas que determinan:
(abcx) = (a’b’c’x’)
Para determinar el elemento homólogo de x operaremos usando perspectividades intermedias entre series que relacionen (seccionan) los elementos de ambos haces.
 Al estudiar la perspectividad vimos que dos series perspectivas (con centro perspectivo el vértice de un hazproyección común), tienen un punto doble que es el que contiene a las bases (intersección de las rectas soportes) de las series.
Al estudiar la perspectividad vimos que dos series perspectivas (con centro perspectivo el vértice de un hazproyección común), tienen un punto doble que es el que contiene a las bases (intersección de las rectas soportes) de las series.
En la figura el punto doble es el D=D’ que contiene a las rectas r y r’ de las series perspectivos con centro perspectivo el punto V.
Esta propiedad es fundamental para conseguir encontrar series perspectivas que relacionen los dos haces proyectivos cuyo tratamiento pretendemos simplificar, como veremos a continuación.
Dados dos haces proyectivos de bases V1 y V2, procederemos a seccionarlos por dos rectas r y r’ determinando series que son perspectivas con dichos haces. Entre los infinitos pares de rectas que podemos utilizar para seccionar estos haces, elegiremos dos que pasen por cualquier punto de intersección de dos elementos homólogos de los haces. El punto D=D’ contiene al par d-d’ de estos haces.
Estas series de puntos de bases r y r’ son perspectivos entre si al ser doble el punto D=D’
El punto Cp es el centro perspectivo de las series de bases r y r’ que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, la construcción para la determinación de elementos homólogas seguirá siendo igualmente válida.
Centro proyectivo
Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“
El punto Cp es el centro perspectivo de las series de bases r y r’, siendo a su vez el centro proyectivo de los haces de bases V1 y V2
Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.
Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.
Geometría Proyectiva





Debe estar conectado para enviar un comentario.