Un des problèmes Clásicos de los Sistemas de Encontrar de Consiste de représentation à l'intersection de deux parties, tels que la détermination du point d'intersection entre une ligne et un plan. Nature topologique sont des problèmes dans lesquels les concepts d'appartenance prévalent.
Les problèmes sont basés sur les relations topologiques sont du type à projection indépendante dans laquelle elles sont.
Intersection: problèmes sont basés sur la détermination des éléments géométriques qui appartiennent à deux éléments simultanément, considérant que ceux-ci sont composées de points infinis.
Nous allons étudier l'étude d'exemple le problème suivant:
Trouver tous les points d'intersection de la ligne r avec le prisme suivant isométrique, indiquant la visibilité de la ligne. Pour résoudre ce problème rappeler précédemment au sein problèmes d'incidence, la détermination du point d'intersection entre une ligne et un plan.
Nous avons vu l' modèle général pour déterminer les systèmes intersections représentation. Dans cette approche, un plan auxiliaire contenant la ligne donnée et nous allons produire une intersection droite avec le plan.
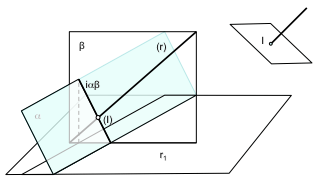
Dans ce genre de problèmes, quand l'intersection est un prisme, nous répétons toujours le problème de l'intersection entre les plans. Par exemple, nous pouvons résoudre en premier lieu intersection d'une ligne avec r un parallélépipède (une boîte avec des côtés parallèles et perpendiculaires). La ligne sera déterminée par la projection directe (r) et la projection sur le plan de la base (r1)
Cela permettra de déterminer un plan contenant la droite, dans ce cas,, est orthogonale à la base. Ceci va produire un plan rectiligne croise le corps qui contient les points d'intersection.
- La détermination de ces lignes se croisent sera basé sur les conditions de parallélisme entre les différents plans du corps, comme un plan en coupe selon deux lignes parallèles aux plans parallèles.
- Si le plan est perpendiculaire à la base, Autres jonction avec les plans perpendiculaires à cela permettra de déterminer rectas Verticales.
Si cuerpo est plus complexe jonction avec quelque chose deberemos résolveur las más de trabajo, Bien que le modèle sera généralement si le très las las caras sont Projection parallèle siendo.
Pour la résolution de cet exercice, la première section de détermination qui provoque le plan contenant la ligne droite r et leur projection sur le plan horizontal XY (r1), donnée sur prismatique. L'points d'entrée et de sortie (1, 2, 3, 4, 5 y 6) sont obtenus comme points d'intersection de la ligne avec ladite section r.
Veremos cómo los más adelante Que résolveur cas tengamos faces obliques.
Sistemas_de_representacion
Doit être lié poster un commentaire.