آؤٹ لک میں Intersections: براہ راست اور cuboids

نمائندگی کے نظام کی کلاسک مسائل میں سے ایک دو عناصر کے تعلق تلاش کرنے کے لئے ہے, اس طرح ایک لائن اور ایک جہاز کے درمیان چوراہے نقطہ کا تعین کرنے کے طور پر. Topological فطرت سے تعلق رکھنے کے تصورات غالب جس میں مسائل ہیں.

مسائل ہیں جس میں آزاد پروجیکشن کی قسم ہیں topological تعلقات پر مبنی ہیں.

چوراہا مسائل کو بیک وقت دو عناصر سے تعلق رکھتے ہیں کہ ہندسی عناصر کا تعین کرنے پر مبنی ہیں, ان لامحدود پوائنٹس پر مشتمل رہے ہیں پر غور.

ہم مثال کے طور پر مطالعہ مندرجہ ذیل مسئلہ کا مطالعہ کریں گے:

isometric دی PRISM کے ساتھ لائن R کی چوراہا کے تمام پوائنٹس تلاش کیجیے, لائن کی نمائش کو اشارہ. اس مسئلہ کو حل کرنے کے لئے پہلے کے اندر اندر یاد واقعات کے مسائل, ایک لائن اور ایک جہاز کے درمیان چوراہے کے نقطہ کا تعین.
ہم نے دیکھا ہے intersections کے نظام کا تعین کرنے کے لئے عام طور پر ماڈل نمائندگی. En este planteamiento haremos pasar un plano auxiliar que contenga a la recta dada y que nos producirá una recta intersección con el plano.

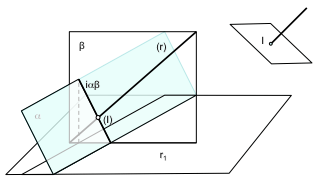
En este tipo de problemas, cuando la intersección sea con un prisma, deberemos repetir sistemáticamente el problema de intersección entre planos. Por ejemplo podemos resolver en primera instancia la intersección de una recta r con un ortoedro (una caja con caras paralelas y perpendiculares entre sí). La recta vendrá determinada por su proyección directa (R) y la proyección sobre el plano de la base (R1)

Para ello determinaremos un plano que contenga a la recta que, اس معاملے میں, sea ortogonal a la base. Este plano producirá unas rectas de intersección con el cuerpo que contendrán a los puntos de intersección.

• La determinación de estas rectas intersección se basará en las condiciones de paralelismo entre los diferentes planos del cuerpo, ya que un plano secciona a dos planos paralelos según rectas paralelas.
• Si el plano es perpendicular a la base, la intersección con otros planos perpendiculares a ésta determinará rectas verticales.

Si el cuerpo es más complejo deberemos resolver las intersecciones con algo más de trabajo, aunque el modelo general será el mismo si las caras siguen siendo paralelas a las de proyección.

Para la resolución de este ejercicio, se determina primero la sección que origina el plano que contiene a la recta r y a su proyección sobre el plano horizontal XY (R1), sobre el cuerpo prismático dado. اندراج اور باہر نکلیں پوائنٹس (1, 2, 3, 4, 5 اور 6) کے ساتھ لائن کی چوراہا کے پوائنٹس کے طور پر حاصل کیا جاتا حصے ر نے کہا ہے کہ.

ہم اسے ترچھا کا سامنا ہے جس میں مقدمات حل کرنے کے لئے کس طرح بعد میں دیکھیں گے.

Sistemas_de_representacion