ال proyecciones principales de la recta sobre dos planos diédricos (planos الأفقي العمودي ذ) يمكن تحديد الطائرات الجديدة الأخرى التوقعات المتعامدة.
سنرى كيف تحدد بشكل عام الإسقاط الجديد من اثنين آخرين. في وقت لاحق وسوف ننظر في طلبك لدراسة ما يسمى “توقعات المساعدة”, مشددا على فائدتها في حل المشاكل المختلفة.
En particular se suele utilizar frecuentemente la denominada “tercera proyección” que se realiza sobre un plano ortogonal a los anteriores denominado plano de perfil. Los tres planos ( أفقي, H, Vertical, في y Perfil, P) determinan un triedro trirrectángulo, en el que se tienen las tres coordenadas (X,و,من) que permiten restituir la información espacial que tengamos representada (proyectada).
Al proyectar sobre un plano, la única coordenada que no se tiene proyectada en esta proyección es la perpendicular a dicho plano.
Si proyectamos sobre el plano horizontal (XY) la coordenada Z la tendremos sobre la proyección vertical, pero también sobre la correspondiente al plano de perfil.
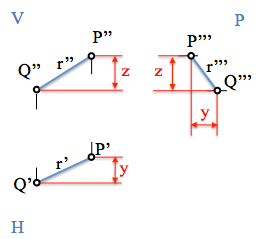
Vemos que dos planos ortogonales comparten una misma coordenada que puede servir para obtener la nueva proyección.
Dadas dos proyecciones sobre planos ortogonales : ¿Cómo podemos obtener la tercera proyección?
Para iniciar la representación que queremos obtener fijaremos un primer punto, P o Q, en la tercera proyección. El otro punto lo fijaremos mediante las cotas relativas que deben mantenerse.
Hemos visto que las proyecciones están vinculadas mediante líneas de referencia. Las nuevas proyecciones, P”’ و س”’ من على التوالي, en tercera proyección, se encontrarán en las correspondientes líneas de referencia, por lo que mantendrán una misma “من” o cota respecto del plano horizontal.
وفي الوقت نفسه, el valor del “alejamiento”, coordenada “و“, respecto del plano vertical, في, se mantiene en la tercera proyección, permitiendo por lo tanto la determinación de los puntos buscados.
Sistemas_de_representacion
يجب أن يكون متصل لإضافة تعليق.