Hemos resuelto la determinación de una cónica definida por sus dos focos y un punto mediante la circunferencia focal de la cónica.
Un problema que usa idénticos conceptos es el de la determinación de una cónica conocidos sus focos y una de sus tangentes. Veremos este problema en el caso de una elipse.
Supongamos que los datos son los focos de una elipse, F1 en F2, y una cualquiera de sus tangentes, t en la figura.
El simétrico de uno de los focos respecto de la tangente debe encontrarse sobre la circunferencia focal de centro el otro foco.
Como la tangente es bisectriz de los radios focales, podemos determinar el punto de tangencia
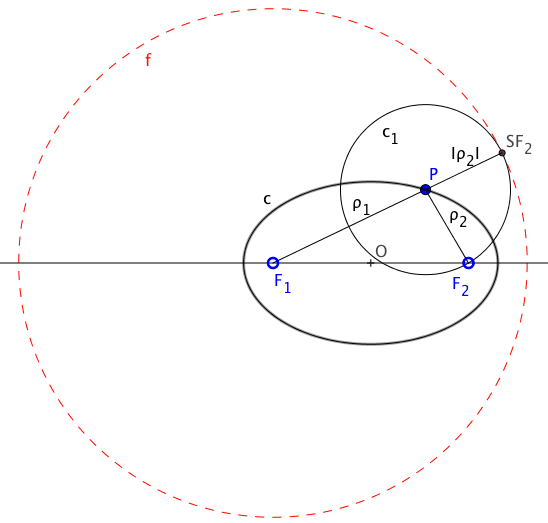
Para determinar los vértices podemos apoyarnos en el valor del radio de la circunferencia focal, 2'n, ya que es la suma, constante, de los dos radios focales de cada punto de la cónica, tal y como vimos en la definición como lugar geométrico de circunferencias tangentes a la focal que pasaban por un punto dado.
Definición de la cónica como lugar geométrico de centros de circunferencias
En este caso si el punto de paso es el de tangencia T, la distancia de este punto al foco que no es centro de la focal (F2) es la misma que la distancia a la circunferencia focal (SF2). El punto T se encontrará en el radio de la circunferencia focal que pasa por el simétrico del otro foco respecto de la tangente.
La cónica está definida por sus elementos principales cuando se conocen los focos y los vértices.
¿Y si en lugar de uno de los focos tuviéramos dos tangentes más? ¿Sabrías encontrar el otro foco?
El problema sería determinar la cónica que viene definida por un foco y tres tangentes.
Moet wees verbind om komentaar te lewer.