Projective ستادوستی: دو projective بنڈل کے Projective مرکز

projective ماڈل میں duality کی قوانین استعمال کرتے ہوئے دوسرے سے پہلے کٹوتی سے خصوصیات اور ڈبل قضیہ کا ایک سیٹ حاصل کر سکتے ہیں. projective کیس کی سیریز میں homologous عناصر حاصل perspectival کی اجازت انٹرمیڈیٹ pespectividades حاصل کرنے کے کی طرف سے کیا گیا تھا ہم نے بلایا ہے کیا حاصل کرتے ہیں “projective محور”. ہم projective بنڈل کی صورت میں دیکھیں گے کہ, دوہری استدلال projective مراکز کا تعین کرنے کے ہماری طرف جاتا ہے.

El “دنیا” پوائنٹس didactically براہ راست ڈبل سے زیادہ سستی ہے, تو ہم نے کے لئے rectilinear سیریز کے ساتھ منسلک تصورات کے ساتھ تجزیہ شروع کر دیا ہے, اب, دوہری فارم کی ترقی میں باہر لے, براہ راست بیم.

ہم اس تحقیق میں ترقی کی رہنمائی میں مدد ملے گی کہ بنیادی سوالات کا ایک سلسلہ کے بارے میں غور کر سکتے ہیں:

• ہم کس طرح دو projective کی وضاحت کرتے ہیں?
• homologous عناصر ایک projectivity تعین کرنے کے لئے ضروری ہیں کتنے
• ہم کس طرح دیا سے homologous عناصر حاصل کر سکتے ہیں?

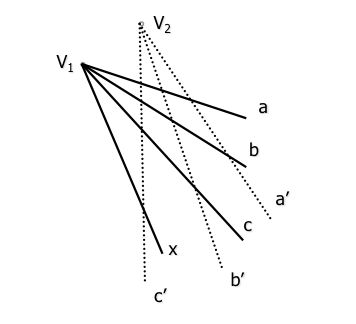
دو projective بنڈل homologous براہ راست کے تین جوڑوں کی وضاحت کرنے کے لئے مقرر ہیں (ایک ایک ', بی بی, C-C '), اپنے اپنے ٹھکانوں پر واقع (ان کے متعلقہ vertices میں شروع).

ایک چوتھی عنصر بیم راس ایکس “V1” ایک نیا ایکس رے ہو گا’ homologue بیم (projective) ڈی بیس (راس) “V1”” quaternions کی صلیب کے تناسب کا تعین کرنے کو برقرار رکھا جاتا ہے تاکہ:

(abcx) = (a'b'c'x ')

ایکس کے homologue تعین کرنے کے لئے perspectividades متعلق سیٹ کے درمیان انٹرمیڈیٹ کا استعمال کرتے ہوئے کام کریں گے (sectioned) دونوں بیم کے عناصر.

مطالعہ میں perspectividad ہم نقطہ نظر کی اس سیریز دیکھا (ایک عام راس hazproyección کے ساتھ نقطہ نظر مرکز), بیس میں موجود ہے کہ ایک ڈبل نقطہ ہے (براہ راست بریکٹ کے تعلق) سیریز.

اعداد و شمار میں ڈبل نقطہ D = D ہے’ ایک براہ راست R اور R پر مشتمل’ وی کے ساتھ perspectival perspectival مرکز نقطہ کی سیریز.

اس کی خاصیت آسان علاج جس کا مطلب ہے دو projective بنڈل منسلک امکانات سیریز کو تلاش کرنے کے لئے ضروری ہے, ذیل میں تبادلہ خیال کے طور پر.

Dados dos haces proyectivos de bases V1 اور V2, دو لائنوں آر اور آر کی طرف سے ان کو کاٹ کرنے کے لئے آگے بڑھنے’ کر رہے ہیں کہ ان کے امکانات کے ساتھ سیریز کا تعین. ہم ان بیم توڑ کرنے کے لئے استعمال کر سکتے ہیں کہ لائنوں کی ان گنت جوڑوں کے درمیان, بیم کے دو homologous عناصر کے تعلق کے کسی بھی موڑ کے ذریعے دو پاسنگ کا انتخاب. نقطہ D = D’ جوڑے پر مشتمل ہے d-d’ ان بیم کی.

Estas series de puntos de bases R اور R 'perspectival ہیں ہر ایک ہونے کی وجہ سے ڈبل نقطہ D = D '

پوائنٹ Cp es el centro perspectivo de las series DE اڈوں R اور R ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, homologous عناصر کے تعین کی تعمیر کا بھی اتنا ہی درست رہے.

Centro proyectivo

Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“

El punto Cp es el centro perspectivo de las series de bases r y r’, کے نتیجے میں کیا جا رہا ہے centro proyectivo de los haces DE اڈوں V1 y V2

Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.

Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.

Projective جیومیٹری