איינער פון די קלאַסיש פּראָבלעמס פון פאַרטרעטונג סיסטעמס איז צו געפינען דעם ינטערסעקשאַן פון צוויי עלעמענטן, אַזאַ ווי דיטערמאַנינג די ינטערסעקשאַן פונט צווישן אַ שורה און אַ פלאַך. טאָפּאָלאָגיקאַל נאַטור זענען פּראָבלעמס אין וואָס די קאַנסעפּס פון בילאָנגינג פּריווייל.
די פּראָבלעמס זענען באזירט אויף טאַפּאַלאַדזשיקאַל באציונגען זענען פרייַ פּרויעקציע טיפּ אין וואָס זיי זענען.
ינטערסעקשאַן פּראָבלעמס זענען באזירט אויף דיטערמאַנינג די דזשיאַמעטריק עלעמענטן וואָס געהערן צו צוויי עלעמענטן סיימאַלטייניאַסלי, קאָנסידערינג אַז די ביסט פארפאסט פון ינפאַנאַט פונקטן.
מיר וועלן לערנען די בייַשפּיל לערנען די ווייַטערדיק פּראָבלעם:
געפינען אַלע פונקטן פון ינטערסעקשאַן פון די שורה ר מיט דער געגעבן פּריסם יסאָמעטריק, ינדאַקייטינג די וויזאַביליטי פון די שורה. צו סאָלווע דעם פּראָבלעם ביז אַהער געדענקען ין ינסידאַנס פּראָבלעמס, דיטערמאַנינג די פונט פון ינטערסעקשאַן צווישן אַ שורה און אַ פלאַך.
מיר האָבן געזען די גענעראַל מאָדעל פֿאַר דיטערמאַנינג ינטערסעקשאַנז סיסטעמען פאַרטרעטונג. אין דעם צוגאַנג, האָבן אַ אַגזיליערי פלאַך מיט די געגעבן שורה און מיר וועלן פּראָדוצירן אַ גלייַך ינטערסעקשאַן מיט די פלאַך.
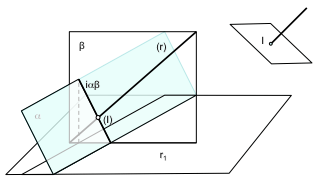
אין דעם מין פון פּראָבלעמס, ווען דער ינטערסעקשאַן איז אַ פּריסם, מיר קאַנסיסטאַנטלי איבערחזרן די פּראָבלעם פון ינטערסעקשאַן צווישן פּליינז. למשל מיר קענען האַלטן אין דער ערשטער בייַשפּיל ינטערסעקשאַן פון אַ שורה ר מיט אַ קובאָיד (אַ קעסטל מיט זייטן פּאַראַלעל און פּערפּענדיקולאַר). די שורה וועט זייַן באשלאסן דורך דירעקט פּרויעקציע (ר) און די פּרויעקציע אַנטו די פלאַך פון די באַזע (ר1)
דאס וועט באַשליסן אַ פלאַך מיט די גלייַך, אין דעם פאַל, איז אָרטאָגאַנאַל צו די באַזע. דאס וועט פּראָדוצירן אַ גלייַך פלאַך ינטערסעקץ מיט דעם גוף, וואס אַנטהאַלטן די פונקטן פון ינטערסעקשאַן.
- די פעסטקייַט פון די שורות ינערסעקט וועט זייַן באזירט אויף די באדינגונגען פון פּעראַלעליזאַם צווישן די פאַרשידענע פּליינז פון דער גוף, ווי אַ פלאַך סעקשאַנד לויט צו צוויי פּאַראַלעל שורות פּאַראַלעל פּליינז.
- אויב די פלאַך איז פּערפּענדיקולאַר צו די באַזע, די ינטערסעקשאַן מיט אנדערע פּליינז פּערפּענדיקולאַר צו דעם ווערטיקאַל שורות באַשליסן.
אויב דער גוף איז מער קאָמפּליצירט ווי מיר האַלטן די ינטערסעקשאַנז מיט עטלעכע מער אַרבעט, כאָטש די קוילעלדיק מוסטער וועט זייַן די זעלבע אויב די פנימער בלייַבן פּאַראַלעל צו די פּרויעקציע.
פֿאַר די האַכלאָטע פון דעם געניטונג, ערשטער דיטערמאַנינג אָפּטיילונג אַז ז די פלאַך מיט די גלייַך שורה ר און זייער פּרויעקציע אויף די האָריזאָנטאַל פלאַך קסי (ר1), געגעבן אויף פּריזמאַטיק. די פּאָזיציע און אַרויסגאַנג פונקטן (1, 2, 3, 4, 5 און 6) ביסט באקומען ווי פונקטן פון ינטערסעקשאַן פון די שורה מיט האט אָפּטיילונג ר.
מיר וועלן זען שפּעטער ווי צו האַלטן קאַסעס אין וועלכע עס פנימער אַבליק.
סיסטעמאַס_דע_רעפּרעסענטאַסיאָן
Debe estar conectado para enviar un comentario.