واحدة من المشاكل الكلاسيكية لنظم التمثيل هو العثور على تقاطع عنصرين, مثل تحديد نقطة تقاطع بين خط وطائرة. الطبيعة الطوبوغرافية هي المشاكل التي تسود مفاهيم الانتماء.
وتستند هذه المشاكل على العلاقات الطوبوغرافية هي نوع الإسقاط المستقلة التي يوجدون فيها.
وتستند مشاكل التقاطع على تحديد العناصر الهندسية التي تنتمي إلى عنصرين في وقت واحد, معتبرا أن هذه تتشكل عن طريق نقطة لانهائية.
سندرس المثال دراسة المشكلة التالية:
البحث فقط عن نقاط تقاطع الخط مع ص موشور معين في المنظور المتعجرف, مشيرا إلى وضوح على التوالي. لحل هذه المشكلة في تذكر سابقا مشاكل الإصابة, تحديد نقطة تقاطع بين خط وطائرة.
شهدنا النموذج العام لتحديد نظم التقاطعات التمثيل. في هذا النهج، لديها الطائرة المساعدة التي تحتوي على خط معين، ونحن سوف تنتج خط مستقيم يتقاطع الطائرة.
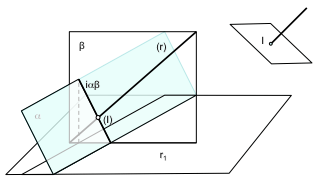
في هذا النوع من المشاكل, عند التقاطع هو موشور, نحن باستمرار تكرار مشكلة التقاطع بين الطائرات. على سبيل المثال يمكننا حل في المقام الأول تقاطع ص تماشيا مع متوازي المستطيلات (مربع مع وجوه متوازية ومتعامدة مع بعضها البعض). وسيتم تحديد الخط بواسطة الإسقاط المباشر (R) والإسقاط على الطائرة من قاعدة (R1)
هذا وسوف يحدد لطائرة تحتوي على الخط, في هذه الحالة, غير متعامد إلى قاعدة. وهذا يتقاطع إنتاج طائرة مستقيم مع الجسم التي تحتوي على نقاط التقاطع.
- وسوف يستند تحديد تقاطع هذه الخطوط على شروط التوازي بين طائرات مختلفة من الجسم, منذ طائرة مقطوع في طائرتين موازية كخطوط متوازية.
- إذا كانت الطائرة عموديا على قاعدة, تقاطع مع الطائرات الأخرى متعامدة مع خطوط عمودية تحديد هذا.
إذا كان الجسد هو أكثر تعقيدا نقوم بحل التقاطعات مع بعض مزيد من العمل, على الرغم من أن النمط العام هو نفسه إذا ظلت وجوه موازية لإسقاط.
لحل هذا التمرين, مصممة القسم الأول الذي يتسبب في الطائرة التي تحتوي على RYA على التوالي توقعاته على المستوى الأفقي XY (R1), على الجسم كما المنشورية. نقاط الدخول والخروج (1, 2, 3, 4, 5 و 6) كما يتم الحصول على نقطة تقاطع الخط مع ذكر القسم ص.
سنرى لاحقا كيفية حل الحالات التي يكون فيها منحدر الوجوه.
Sistemas_de_representacion
يجب أن يكون متصل لإضافة تعليق.