 El estudio de las cónicas se puede realizar desde diferentes enfoques geométricos. Uno de las análisis más usado es el que las determina a partir de secciones planas en un cono de revolución.
El estudio de las cónicas se puede realizar desde diferentes enfoques geométricos. Uno de las análisis más usado es el que las determina a partir de secciones planas en un cono de revolución.
A partir de esta definición es posible inferir propiedades métricas de estas curvas, además de nuevas definiciones de las mismas.
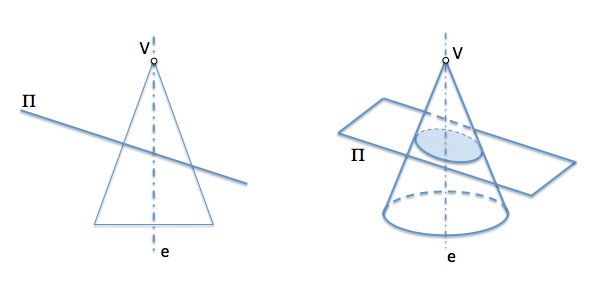
Utilizaremos para el análisis el caso en el que la curva resultado de la sección plana en un cono de revolución es una elipse. En este caso el ángulo que formaba el plano de la sección con el eje del cono era mayor que el semiángulo en el vértice.
Posteriormente se podrá analizar de forma similar los casos en los que la curva sea una parábola o una hipérbola.
Sea por lo tanto un cono de revolución de vértice “في” y eje “و”, que se ha seccionado por un plano que no pase por su vértice. Este plano determina una curva que supondremos es una elipse para nuestro estudio.
Si consideramos una esfera tangente al plano y, معا, a la superficie cónica, con su centro por lo tanto en el eje de esta forma geométrica. Esta esfera tendrá en contacto con el cono una circunferencia “ج” contenida en un plano perpendicular a su eje “و”. La intersección de este plano con el que produce la sección es una recta que denominaremos directriz “د” de la cónica.
Al punto de contacto entre la esfera y el plano que contiene a la curva le denominaremos “Foco de la cónica”.
Al punto de la cónica que se encuentra en el plano de simetría del conjunto le denominaremos “Vértice de la cónica”
En el caso de la elipse podemos determinar una segunda esfera, por lo que esta curva tendrá dos vértices, dos focos y dos directrices.
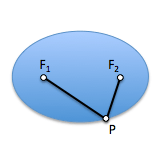
Si consideramos un punto “P” cualquiera de la curva y las distancias desde este punto a los focos de la elipse, PF1 و PF2, podemos determinar una propiedad métrica de esta curva que nos dará paso a una definición muy útil de la misma.
Como las tangentes desde un punto P a una esfera tienen igual longitud, se cumplirá que las tangentes desde P a la primera esfera, PF1 y PM, miden lo mismo. De igual forma ocurrirá con las tangentes desde este punto a la segunda esfera, PF2 y PN.
Por ello podemos determinar que la suma de estas dos distancias, PF1 y PF2, es igual a la distancia MN sobre la generatriz del cono limitada por los planos que contienen a las circunferencias de contacto c1 y c2.
Esto nos permite dar una definición de la elipse como la siguiente:
La Elipse es el lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos, denominados Focos, tiene un valor constante.
Si consideramos a los vértices de la cónica como puntos de este lugar geométrico es fácil demostrar que la distancia de un foco a un vértice es igual a la distancia del otro foco al otro vértice y, con ello, demostrar que la suma de las distancias de un punto de la elipse a los focos es igual a la distancia entre los vértices de la cónica.






يجب أن يكون متصل لإضافة تعليق.