見通しの交差点: ストレートと立方体

表現系の古典的な問題の一つは、2つの要素の交点を見つけることである, そのような線と平面との交点を決定することとして. トポロジカルな性質は、所属の概念が優先する問題である.

問題は、それらが独立した投射型である位相関係に基づいている.

交差点の問題は、同時に二つの要素に属している幾何学的な要素を決定することに基づいている, これらは無限のポイントで構成されていることを考慮すると.

私たちは、研究事例を、以下のような問題を検討する:

アイソメトリック与えられたプリズムと線Rの交点のすべてのポイントを見つける, ラインの視認性を示す. この問題を解決するために、以前内に思い出す 発生率の問題, 線と平面との交点を求める.
我々は見てきました 交差点システムを決定するための一般的なモデル 表現. このアプローチでは、与えられた行を含む補助平面を持っていると我々は平面と直線の交点が生成されます.

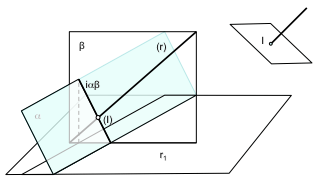
問題はこの種の, 交点がプリズムであるとき, 我々は一貫して平​​面との交点の問題を繰り返す. 例えば、我々は最初のインスタンスに解決することができます 直方体とラインRの交点 (パラレルおよび垂直辺の箱). ラインは直接投影によって決定されます (R) ベースの平面へと投影 (R1)

これはストレートを含む平面を決定します, この場合, 基部に対して直交している. これは直平面を生成します交差点のポイントを含むボディと交差.

• これらの線の交差判定は、身体の異なる面間の平行度の条件に基づいて説明する, 2本の平行線平行な平面に従って切片面として.
• 平面は基部に対して垂直である場合, 他の面との交点は、この垂直線に垂直決定.

ボディは、我々はいくつかのより多くの仕事との交差を解消よりも複雑である場合, 顔が投影と平行残っている場合全体的なパターンは同じになりますが、.

この演習の解決のため, 水平面XY上の直線がrとその突起を含む平面を引き起こす第1の判定部 (R1), プリズムに与えられた. 入口と出口のポイント (1, 2, 3, 4, 5 Y 6) セクションRは言ったラインの交点として得られる.

我々は、それが斜めに直面するケースを解決する方法を後で見る.

Sistemas_de_representacion