Один из классических проблемы представления систем, чтобы найти пересечение двух элементов, например, для определения точки пересечения между линией и плоскостью. Топологического характера задачи, в которых понятия принадлежащих преобладают.
Эти проблемы на основе топологических отношений являются независимыми проекционного типа, в которых они.
Пересечение проблемы на основе определения геометрических элементов, которые принадлежат к двум элементам одновременно, учитывая, что эти состоят из бесконечного пунктов.
Мы будем изучать на примере исследования следующую задачу:
Найти все точки пересечения линии R с данным призму изометрической, указывающие видимость линии. Чтобы решить эту проблему ранее помните, в течение Заболеваемость проблемы, определения точки пересечения между линией и плоскостью.
Мы видели, общая модель для определения пересечений систем представление. При таком подходе имеют вспомогательные плоскости, содержащей данную линию, и мы будем производить прямой пересечения с плоскостью.
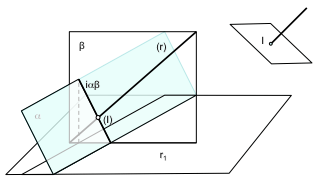
В такого рода проблемы, когда пересечение представляет собой призму,, мы последовательно повторить проблема пересечения между плоскостями. Например, мы можем решать в первую очередь пересечение прямой R с кубовидной (коробка со сторонами, параллельными и перпендикулярными). Линия будет определяться прямой проекции (R) и проекции на плоскости основания (R1)
Это позволит определить плоскость, содержащая прямые, В этом случае, ортогональной базы. Это приведет к прямой плоскость пересекает с телом, которые содержат точки пересечения.
- Определение этих линий пересекаются будет основываться на условиях параллелизм между разных плоскостях тела, в виде плоской разрезом по двум параллельным линиям параллельных плоскостях.
- Если плоскость перпендикулярна к основанию, пересечения с другими плоскостях, перпендикулярных к этой вертикальной линии определить.
Если тело является более сложным, чем мы решим пересечений, немного поработав, хотя общий шаблон будет таким же, если лица остаются параллельными проекциям.
Для разрешения этого упражнения, первая секция определения, которое вызывает плоскость, содержащая прямые линии R и их проекции на горизонтальную плоскость XY (R1), представленными на призматических. Точки входа и выхода (1, 2, 3, 4, 5 год 6) получаются как точки пересечения линии с указанной секцией т.
Позже мы увидим, как разрешить случаи, в которых она сталкивается косой.
Sistemas_de_representacion
Должно быть связано добавить комментарий.