פּראָדזשעקטיווע דזשיאַמאַטרי: פּראָדזשעקטיווע צענטער פון צוויי פּראָדזשעקטיווע באַנדאַלז

ניצן די געזעצן פון דואַליטי אין פּראָדזשעקטיווע מאָדעלס קענען באַקומען אַ סכום פון פּראָפּערטיעס און צווייענדיק טהעאָרעמס פון אנדערע פריער דידאַקטיד. באקומען האָמאָלאָגאָוס יסודות אין די פּראָדזשעקטיווע פאַל סעריע איז געטאן דורך באקומען ינטערמידייט פּעספּעקטיווידאַדעס ערלויבט פּערספּעקטיוואַל טאָן מיר באַקומען וואָס מיר האָבן גערופן “פּראָדזשעקטיווע אַקס”. מיר וועלן זען אַז אין דעם פאַל פון פּראָדזשעקטיווע באַנדאַלז, צווייענדיק ריזאַנינג פירט אונדז צו באַשטימען פּראָדזשעקטיווע סענטערס.

די “וועלט” ווייזט איז מער אַפאָרדאַבאַל ווי דידאַקטיקאַללי גלייַך צווייענדיק, אַזוי מיר האָבן סטאַרטעד די אַנאַליסיס מיט די קאַנסעפּס פארבונדן מיט רעקטילינעאַר סעריע פֿאַר, איצט, פירן אויס אַנטוויקלונג אין צווייענדיק פארמען, גלייַך בימז.

מיר קענען באַטראַכטן אין דעם לערנען אַ סעריע פון ​​יקערדיק שאלות אַז וועט העלפן פירן די אַנטוויקלונג:

• ווי טאָן מיר דעפֿינירן צוויי פּראָדזשעקטיווע?
• ווי פילע האָמאָלאָגאָוס עלעמענטן זענען דארף צו באַשליסן אַ פּראָדזשעקטיוויטי
• ווי קענען מיר קריגן האָמאָלאָגאָוס יסודות פון געגעבן?

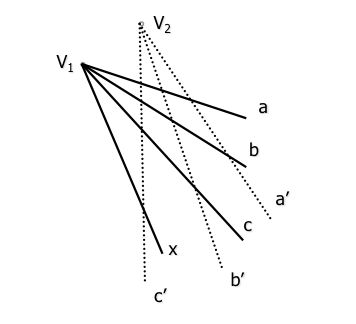
צוויי פּראָדזשעקטיווע באַנדאַלז זענען באשלאסן צו דעפֿינירן דרייַ פּערז פון האָמאָלאָגאָוס גלייַך (א אַ ', B-ב ', C-C '), ליגן אויף זייער ריספּעקטיוו באַסעס (ערידזשאַנייטינג אין זייער ריספּעקטיוו ווערטיסעס).

א פערט עלעמענט שטראַל ווערטעקס רענטגענ “V1” וועט האָבן איין נייַ שטראַל רענטגענ’ האָמאָלאָגוע שטראַל (פּראָדזשעקטיווע) דע באַזע (ווערטעקס) “V1”” אַזוי אַז די קרייַז פאַרהעלטעניש פון קוואַטערניאָנס איז ריטיינד דיטערמאַנינג:

(אַבקקס) = (אַ'ב'ק'קס ')

צו באַשטימען די האָמאָלאָגוע פון ​​רענטגענ וועט אַרבעטן ניצן ינטערמידייט צווישן שטעלט אַז פאַרבינדן פּערספּעקטיווידאַדעס (סעקשאַנד) עלעמענטן פון ביידע בימז.

אין געלערנט די פּערספּעקטיוויטי מיר געזען אַז סעריע פון ​​פּערספּעקטיווז (פּערספּעקטיוו צענטער מיט אַ פּראָסט ווערטעקס האַזפּרויעקסיóן), האָבן אַ טאָפּל פונט וואָס איז קאַנטיינד אין די באַזע (ינטערסעקשאַן פון די גלייַך בראַקאַץ) סעריע.

אין די פיגורע די טאָפּל פונט איז די = די’ מיט אַ גלייַך ר און ר’ סעריע פון ​​פּערספּעקטיוואַל פּערספּעקטיוואַל צענטער פונט מיט V.

דעם פאַרמאָג איז יקערדיק פֿאַר געפונען פּראַספּעקץ סעריע פֿאַרבינדונג די צוויי פּראָדזשעקטיווע באַנדאַלז וואָס מיטל סימפּלאַפייד באַהאַנדלונג, ווי דיסקאַסט ונטער.

Dados dos haces proyectivos de bases V1 און V2, גיינ ווייַטער צו שנייַדן זיי דורך צוויי שורות ר און ר’ דיטערמאַנינג סעריע מיט די פּראַספּעקץ אַז זענען טאן. צווישן די קאַונטלאַס פּערז פון שורות אַז מיר קענען נוצן צו ייַנריס די בימז, קלייַבן צוויי גייט פארביי דורך קיין פונט פון ינטערסעקשאַן פון צוויי האָמאָלאָגאָוס יסודות פון די בימז. די פונט די = די’ כּולל די פּאָר d-d’ פון די בימז.

Estas series de puntos de bases ר און ר 'זענען פּערספּעקטיוואַל יעדער זייַענדיק טאָפּל פונט די = די '

פונט Cp es el centro perspectivo de las series דע באַסעס ר און ר ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, קאַנסטראַקשאַן פֿאַר באַשטימונג פון האָמאָלאָגאָוס יסודות בלייַבן גלייַך גילטיק.

Centro proyectivo

Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“

El punto Cp es el centro perspectivo de las series de bases r y r’, זייַענדיק אין דרייַ די centro proyectivo de los haces דע באַסעס V1 y V2

Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.

Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.

פּראָדזשעקטיווע געאָמעטרי