Изучение коники может быть изготовлена из различных геометрических подходов. Один из наиболее часто используемых анализов - это тот, который определяет их по плоские сечения в конусе вращения.
Из этого определения можно сделать вывод, метрические свойства этих кривых, в дополнение к новым определениям того же.
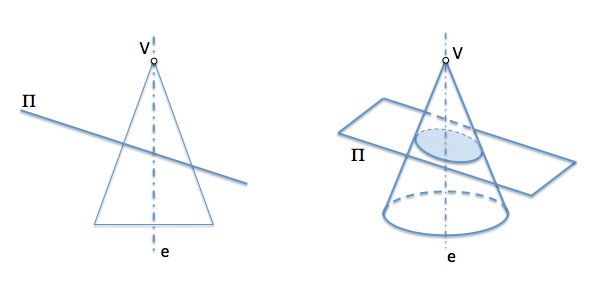
Мы будем использовать для анализа случай, когда кривая, полученная в результате плоского сечения в конусе вращения, представляет собой эллипс. При этом угол, образованный плоскостью сечения с осью конуса, был больше половины угла при вершине.
Позже можно будет аналогичным образом проанализировать случаи, когда кривая представляет собой параболу или гиперболу..
Пусть поэтому - вершинный конус вращения “V” и ось “и”, который был рассечен плоскостью, не проходящей через его вершину. Эта плоскость определяет кривую, которую мы будем считать эллипсом для нашего исследования..
Если рассматривать сферу, касательную к плоскости y, одновременно, к конической поверхности, с центром, следовательно, на оси этой геометрической формы. Эта сфера будет иметь окружность, контактирующую с конусом. “C” содержится в плоскости, перпендикулярной его оси “и”. Пересечение этой плоскости с плоскостью, образующей сечение, представляет собой линию, которую мы назовем директрисой. “ре” конический.
Мы будем называть точку контакта между сферой и плоскостью, содержащей кривую “Фокус конический”.
Точку коники, лежащую в плоскости симметрии множества, назовем “Вершина конический”
В случае эллипса мы можем определить вторую сферу, так что эта кривая будет иметь две вершины, dos focos y dos directrices.
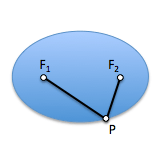
Si consideramos un punto “P” cualquiera de la curva y las distancias desde este punto a los focos de la elipse, PF1 год PF2, podemos determinar una propiedad métrica de esta curva que nos dará paso a una definición muy útil de la misma.
Como las tangentes desde un punto P a una esfera tienen igual longitud, se cumplirá que las tangentes desde P a la primera esfera, PF1 y PM, miden lo mismo. De igual forma ocurrirá con las tangentes desde este punto a la segunda esfera, PF2 y PN.
Por ello podemos determinar que la suma de estas dos distancias, PF1 y PF2, es igual a la distancia MN sobre la generatriz del cono limitada por los planos que contienen a las circunferencias de contacto c1 y c2.
Esto nos permite dar una definición de la elipse como la siguiente:
La Elipse es el lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos, denominados Focos, tiene un valor constante.
Si consideramos a los vértices de la cónica como puntos de este lugar geométrico es fácil demostrar que la distancia de un foco a un vértice es igual a la distancia del otro foco al otro vértice y, con ello, demostrar que la suma de las distancias de un punto de la elipse a los focos es igual a la distancia entre los vértices de la cónica.
Должно быть связано добавить комментарий.