表示系統的經典問題之一是要找到兩個元素的交點, 如確定一條線和一個平面的交點. 拓撲性質問題屬於概念為準.
問題是基於拓撲關係是獨立的投影類型中，他們.
路口的問題的基礎上確定的幾何元素，同時屬於兩個元素, 考慮，這些都是無限的點組成.
我們會研究實例研究以下問題:
查找與棱鏡等距點相交的線r, 指示線的可見性. 為了解決這個問題，以前記得在 發生問題, 確定一條線和一個平面之間的交叉點.
我們已經看到了 確定交叉口系統的一般模型 表示. 在這種方法中，有一個包含給定的行的輔助平面，我們將產生一個與平面的直線交點.
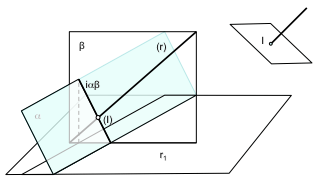
在這樣那樣的問題, 時的交叉點是棱鏡, 我們一貫飛機之間的重複交叉問題. 例如，我們可以在第一時間解決 相交的線為r與長方體 (一個盒子兩側平行和垂直). 將由直接投影線 (ŗ) 和鹼的平面上的投影 (R1)
這將確定一個平面，包含直, 在這種情況下，, 是正交的基. 這將產生一個直平面相交的身體包含的交叉點.
- 這些線相交的測定將根據身體的不同的平面之間的平行度的條件, 根據兩條平行的直線平行的平面剖開的平面.
- 如果平面是垂直於基, 與其他的平面的交點垂直於該垂直線確定.
如果身體更複雜，比我們一些更多的工作與解決的交點, 雖然整體的方式將是相同的，如果面保持平行的投影.
對於這次演習的決議, 第一確定部分所引起的平面中的直線r與水平平面XY上的投影 (R1), 棱柱. 進入和退出點 (1, 2, 3, 4, 5 和 6) 得到點的交叉點的線與所述R節.
我們稍後會看到如何解決案件中，面臨著斜.
Sistemas_de_representacion
一定是 連接的 發表評論.