Conique définie par les deux foyers et une tangente

Hemos resuelto la determinación de una cónica definida por sus dos focos y un punto mediante la circunferencia focal de la cónica.

Un problème qui utilise des concepts identiques est celui de déterminer une conique avec ses foyers et une de ses tangentes connues. Nous verrons ce problème dans le cas d'une ellipse.

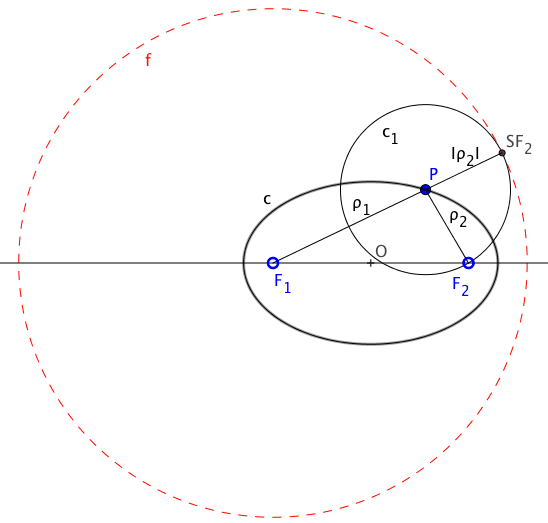
Supongamos que los datos son los focos de una elipse, F1 y F2, y una cualquiera de sus tangentes, t la figure.

El simétrico de uno de los focos respecto de la tangente debe encontrarse sobre la circunferencia focal de centro el otro foco.

Como la tangente es bisectriz de los radios focales, podemos determinar el punto de tangencia

Para determinar los vértices podemos apoyarnos en el valor del radio de la circunferencia focal, 2à, ya que es la suma, constante, des deux rayons focaux de chaque point de la conique, comme nous l'avons vu dans le définition comme lieu de circonférences tangent au point focal passant par un point donné.

Définition de la conique comme lieu de centres de circonférences

Dans ce cas, si le point de passage est la tangence T, la distance entre ce point et la mise au point qui n'est pas le centre de la mise au point (F2) est la même que la distance à la circonférence focale (SF2). Le point T se trouvera dans le rayon du cercle focal qui passe par le symétrique de l'autre foyer par rapport à la tangente.

La conique est définie par ses principaux éléments lorsque les foyers et les sommets sont connus.

Et si au lieu de l'un des foyers, nous avions deux tangentes supplémentaires? Sauriez-vous comment trouver l'autre foyer?

Le problème serait de déterminer la conique qui est définie par un foyer et trois tangentes.

GEOMETRÍA MÉTRICA