 שימוש בחוקים של דואליות בדגמים השלכתית יכול לקבל סט של תכונות ומשפטים כפולים מאחרים שנוכה בעבר. קבלת אלמנטים הומולוגיים במקרה הסדרה השלכתית בוצע על ידי קבלת pespectividades ביניים אפשר פרספקטיבי אנחנו מקבלים מה שאנחנו קוראים “ציר השלכתית”. אנו רואים כי במקרה של חבילות השלכתית, חשיבה דואלית מובילה אותנו כדי לקבוע מרכזים השלכתית.
שימוש בחוקים של דואליות בדגמים השלכתית יכול לקבל סט של תכונות ומשפטים כפולים מאחרים שנוכה בעבר. קבלת אלמנטים הומולוגיים במקרה הסדרה השלכתית בוצע על ידי קבלת pespectividades ביניים אפשר פרספקטיבי אנחנו מקבלים מה שאנחנו קוראים “ציר השלכתית”. אנו רואים כי במקרה של חבילות השלכתית, חשיבה דואלית מובילה אותנו כדי לקבוע מרכזים השלכתית.
El “עולם” נקודות היא זולה יותר מכפול דידקטית ישר, כך התחלנו את הניתוח עם המושגים הקשורים לסדרה מרובעת עבור, עכשיו, לבצע את הפיתוח בצורות כפולה, קורות ישרות.
אנחנו יכולים לשקול במחקר זה סדרה של שאלות בסיסיות שתעזור לכוון את הפיתוח:
- כיצד אנו מגדירים שני השלכתית?
- כמה אלמנטים הומולוגיים נחוצים כדי לקבוע טליות
- איך אנחנו יכולים להשיג אלמנטים הומולוגיים מניתנו?
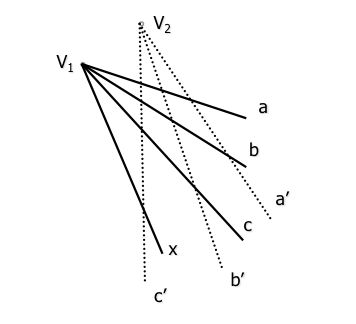
שתי חבילות השלכתית נקבעות להגדיר שלושה זוגות ישרים הומולוגיים (-', ב-b ', c-c '), ממוקם בבסיסים שלהם בהתאמה (שמקורו בקודקודים שלהם).
X קודקוד קרן היסוד רביעי “V1” יהיה x ray החדש אחד’ קרן homologue (הטלי) בסיס דה (קדקוד) “V1”” כך שהיחס הצולב של quaternions נשמרים קביעה:
(abcx) = (a'b'c'x ')
כדי לקבוע את homologue של x יפעל באמצעות ביניים בין סטים המתייחסים perspectividades (מחולק) אלמנטים של שני הקורות.
 בלימוד perspectivity ראינו סדרה של נקודות מבט (מרכז פרספקטיבה עם hazproyección קודקוד משותף), יש נקודה כפולה שכלולה בבסיס (צומת של סוגריים הישרים) סדרה.
בלימוד perspectivity ראינו סדרה של נקודות מבט (מרכז פרספקטיבה עם hazproyección קודקוד משותף), יש נקודה כפולה שכלולה בבסיס (צומת של סוגריים הישרים) סדרה.
בדמות הנקודה הכפולה היא D = D’ המכיל r ו R ישר’ סדרה של נקודת מרכז פרספקטיבי פרספקטיבי עם V.
מאפיין זה הוא חיוני לסדרת סיכויים למצוא קישור שתי חבילות השלכתית מה שאומר שטיפול פשוט יותר, כפי שנראה להלן.
Dados dos haces proyectivos de bases V1 ו - V2, להמשיך לחתוך אותם על ידי r שני קווים וr’ קביעת סדרה עם אותם לקוחות פוטנציאליים, כי הם עושים. בקרב זוגות רבים מספור של קווים שאנו יכולים להשתמש בו כדי לנתק את הקורות הללו, לבחור שני עוברים דרך כל נקודת חיתוך של שני אלמנטים הומולוגיים של הקורות. נקודת D = D’ מכיל הזוג d-d’ קורות אלה.
Estas series de puntos de bases r ור 'הם פרספקטיבי כל נקודה כפולה להיות D = ד '
הנקודה Cp es el centro perspectivo de las series בסיסי דה r ו - ר ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, הבנייה לקביעת אלמנטים הומולוגיים תישאר בתוקף באותה המידה.
Centro proyectivo
Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“
El punto Cp es el centro perspectivo de las series de bases r y r’, להיות בתורו centro proyectivo de los haces בסיסי דה V1 y V2
Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.
Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.
הטלי גיאומטריה





חייב להיות מְחוּבָּר לפרסם תגובה.