GeoGebra의 동적 기하 구조의 견고성: 원의 포인트의 극성

고전 기하학 분야의 연구는 동적으로 변경 될 수있는 구성을 할 수있는 도구를 이용하여 보강 될 수있다: 변분 구조.

Estas construcciones pueden servir para que entendamos cómo se mantienen determinadas propiedades en las relaciones geométricas que denominaremos “Invariantes”, así como para verificar que determinados conceptos que damos como axiomas son válidos simplemente en determinadas condiciones. También nos ayuda a entender cómo varía una representación al cambiar la disposición de los elementos que intervienen en la misma, facilitando la generalización y comprensión profunda de los fundamentos geométricos.

도구 “브라” 그것은 우리가 기하학적 추론에서 사용하는 건물의 견고성을 보장하기 위해이 개념을 설명하고 기하학적 관계의 상세한 지식의 중요성을 설명하는 역할을합니다, ya que, 때때로, 일부 구조물은 타당성을 잃을 수 있습니다.

원의 포인트의 극성.

Veremos con un ejemplo relativamente sencillo cómo la utilización de una u otra construcción puede conducirnos a situaciones en los que la geometría mas básica deja de ser de aplicación.

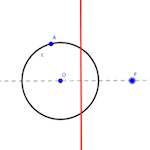
Supongamos que tenemos una 둘레 “C” 센터 “O” que pasa por un determinado punto “A”, 그리고 포인트 “피” que en principio es exterior a esta circunferencia.

A partir de estos datos nos planteamos determinar una 똑 바른 que sea la polar de P respecto de la circunferencia c.

¿Qué es la polar de un punto respecto de una circunferencia? La respuesta a esta pregunta nos puede conducir a una u otra construcción geométrica.

Es el lugar geométrico de los extremos de los diámetros de las circunferencias que pasando por el punto P son ortogonales a la circunferencia c.

Las circunferencias que pasan por un punto y son ortogonales a otra circunferencia se encuentran agrupadas en un haz de circunferencias. Si consideramos al punto como una circunferencia de radio nulo, los centros estarán en el eje radical de la circunferencia y el punto determinando un 타원형의 빔 주위 (conjugado del hiperbólico formado por la circunferencia c y el punto P)

Para determinar este lugar geométrico podemos obtener un punto de paso ya que sabemos que es una recta perpendicular al diámetro de la circunferencia c que con tiene al punto P (perpendicular a la recta O-P).

Mediante una recta tangente desde P a la circunferencia podemos obtener el punto T de tangencia por el que pasará la polar. La determinación de un arco capaz 으로 90 grados (ángulo recto) entre el punto P y el centro O nos permitirá obtener este punto T de tangencia por el que pasará la recta polar.

La circunferencia de diámetro PT es ortogonal a la circunferencia c ya que sus radios en el punto T de contacto son ortogonales por lo que T cumple con el lugar geométrico que hemos usado para definir la recta polar.

Sin embargo esta construcción tan sencilla pierde su validez en el momento en el que el punto P pasa a ser interior a la circunferencia c, como puede observarse en la siguiente figura, ya que el arco capaz no corta a la circunferencia c. Deberemos buscar nuevos modelos que resuelvan estas posiciones.

Es el lugar geométrico de los puntos conjugados de P respecto de la circunferencia c.

Recordaremos que una cuaterna de puntos (ABCD) cuyo valor es la unidad negativa se denomina cuaterna armónica, 즉:

(ABCD)=-1

Siendo

(ABCD) = (ACD)/(BCD) = (AC/AD)/(BC/BD)

En su momento definíamos la polar de un punto P respecto de dos rectas a y b como el lugar geométrico de los conjugados del punto P respecto de los de intersección con “a” 과 “B” del haz de rectas con vértice en P.

A partir de la geometría del 전체 cuadrivertice podíamos obtener la recta que cumplía las condiciones solicitadas, siendo (PP ’ AB)=-1.

Este modelo nos permite realizar una nueva construcción para determinar la polar respecto de la circunferencia mediante el cuadrivértice ABCD que se puede obtener con un diámetro de la circunferencia y la cuerda AD resultado de proyectar desde P el punto A que determina el radio de nuestra circunferencia. 이 경우:

(PP1AD)=(PP2BC)=-1

luego la recta que pasa por los puntos diagonales del cuadrivértice (D1 및 D2) es el lugar geométrico buscado.

Al modificar la posición del punto P se conserva la robustez del modelo, en el que ademas no ha sido necesario utilizar ninguna circunferencia (solución lineal).

Existen otras soluciones que pueden ser híbridas entre las anteriores, en las que se pueden utilizar circunferencias auxiliares para determinar ejes radicales que impliquen la ortogonalidad, sabiendo que la recta O-P es además el eje radical del haz conjugado. Se deja al lector el análisis de esta nueva y simple construcción.

Modelo variacional con GeoGebra

Para terminar se añade el fichero Geogebra con la geometría dinámica que permitirá al lector experimentar variando las posiciones de los elementos.

¿Sabrías realizar una nueva construcción robusta que permitiera variar las posiciones de los elementos sin perder su validez?

메트릭 형상