Конусный как локус центры окружностей касательные

Мы видели, что изучение коники могут быть сделаны из различных геометрических подходов.

Особенно, al iniciar el análisis de las cónicas hemos definido la elipse como lugar geométrico, мы сказали, что:

La Elipse es el lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos, denominados Focos, tiene un valor constante.

Esta definición métrica de esta importante curva nos permite abordar su estudio relacionándolo con el de las circunferencias tangentes, conocido como el “Проблема Аполлония” en alguna de sus versiones. Cuando abordemos el estudio de las parábola o de la hipérbola volveremos a replantear el problema para generalizar estos conceptos y reducir los problemas al “Problema fundamental de tangencias en el caso recta“, o el “Problema fundamental de tangencias en el caso circunferencia“, а именно, la determinación de una circunferencia de un “Haz corradical” con una condición de tangencia.

Supongamos, aplicando la definición anterior de la elipse, que los puntos fijos son F1 год F2. Estos puntos son los focos de la elipse. Supongamos además que la cónica se termina de definir por la condición de paso por un punto dado P.

Según la definición anterior la suma de distancias desde P a los dos focos debe ser constante. Llamaremos a esa suma “2a”.

ρ1 + ρ2 = 2a = constante

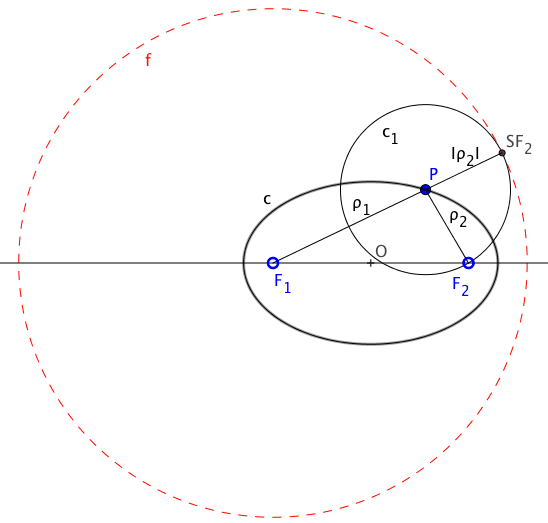
Si llevamos el segmento ρ2 a continuación del punto P según la dirección del segmento ρ1, obtendremos un punto “SF2” que dista del foco F1 el valor “2a“.

Al obtener todos los puntos de la cónica, como la suma de distancias a los focos es “2a“, los puntos similares al “SF2” se encontrarán a esa distancia (2a) del foco F1, por lo que se encontrarán en una circunferencia denominada “фокусное окружности эллипса“.

Фокусное круг конуса является то, что длина окружности, центр которого в одном из фокусов и его радиус равен расстоянию между вершинами конической (2a)

Так как расстояние от точки P сосредоточиться F2 является координационным центром, Это совпадает с точкой “SF2”, обхват которая имеет свой центр в точке P и радио el valor “ρ2” пройдет мимо “SF2” координационный центр окружности, но и в качестве центров “F1” очаговый и “P” эта новая окружность выровнены с общей точкой обоих “SF2”, эта точка касания между двумя кругами, что позволяет сделать вывод о том, что:

Точки эллипса являются центрами окружностей, являющихся касательным к фокальной окружности, Они проходят через другой фокус.

Это определение коники позволяет нам решать задачи определения касательных и точек пересечения или касательной к коническому пути решения проблем касательных.

Например, определения точки пересечения линии с коническим определяются окружности, имеющие свой центр на линии, проходящей через фокус и касательной к фокальной окружности. Имея свой центр на линии и пройти через фокус, Он будет проходить через указанный симметрично относительно линии фокуса и задачи сводится найти окружности, проходящей через две точки (фокус и симметричный) Они касаются фокусного, а именно, две путевые точки (принадлежности к эллиптическому лучу) и условие касания окружности фокальной: Фундаментальной проблемой касательные.

Как мы получаем точки, мы можем связать прямые касательные и точки касания, как показано на рисунке ниже. Поскольку линия “R” касательной к конической, мы можем сделать вывод, что “Рассекайте” координационные радио ρ1 год ρ2, как описано ниже.

Вы бы быть в состоянии удержать вас?

Метрическая геометрия