Para representar un objeto en el sistema diédrico normalmente usaremos la proyecciones sobre los tres planos del triedro de referencia, tal y como hemos visto al estudiar los fundamentos del sistema diédrico.
一般来说，仅使用三个可能的计划中的两个就足够了。, 例如，直线由其在水平和垂直平面上的投影表示。. 有时可能会很方便, 甚至是必要的, 根据不同的投影方向得到新的投影, 在这种情况下我们会称它们为 “辅助突起” .
Supongamos que queremos obtener un nuevo plano de proyección que sustituya al plano vertical. Vemos que cualquier plano perpendicular al plano horizontal, como son el vertical y el de perfil, comparten la dirección normal a este plano y en consecuencia la coordenada “从”,
Si definimos un nuevo plano vertical “V1” también compartirá esta coordenada “从” que será necesaria para obtener la proyección auxiliar.
Supongamos que tenemos las proyecciones diédricas de una recta sobre sus planos horizontal y vertical.
Al realizar un nuevo plano vertical, como se ha visto, se conservará la coordenada “从” relativa entre cada pareja de puntos de la proyección. Podemos determinar las coordenadas relativas de los puntos de la recta según esta dirección.
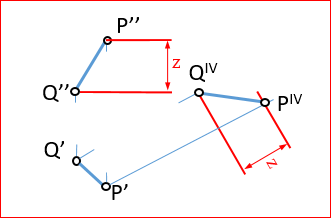
Supongamos que la nueva proyección está definida de forma que el punto “Q” se proyecta según “QIV” (proyección cuarta del punto Q)
Obtendremos las nuevas proyecciones de los puntos ya que se situarán sobre sus respectivas líneas de referencia con la proyección previa (en este caso la primera proyección o proyección horizontal) y además se conservarán las cotas relativas sobre el nuevo plano de proyección (en este caso la “从”).
Para completar el estudio sólo falta determinar la mejor dirección para realizar la proyección auxiliar. Veremos cómo elegir esta dirección para poder situar los elementos paralelos o perpendiculares a las nuevas proyecciones, simplificando problemas de medida lineal o angular entre rectas y planos.
一定是 连接的 发表评论.