Προβολική Γεωμετρία: Προβολική κέντρο δύο προβολικές δέσμες

Χρησιμοποιώντας τους νόμους της δυαδικότητας σε προβολικές μοντέλα μπορούν να πάρουν ένα σύνολο ιδιοτήτων και διπλή θεωρήματα από άλλους που είχαν αφαιρεθεί προηγουμένως. Η απόκτηση ομόλογο στοιχεία στο προβολικό σειρά υπόθεσης έγινε με την απόκτηση ενδιάμεσων pespectividades επιτρέπεται perspectival παίρνουμε αυτό που έχουμε ονομάσει “άξονα προβολικές”. Θα δούμε ότι σε περίπτωση προβολικές δέσμες, Διπλή συλλογιστική μας οδηγεί να προσδιορίσει τα κέντρα προβολικές.

Ο “κόσμος” σημεία είναι πιο προσιτές από ό, τι διδακτικά ευθεία διπλή, έτσι έχουμε ξεκινήσει την ανάλυση με τις έννοιες που συνδέονται με ευθύγραμμα σειρά για, τώρα, διενεργεί την ανάπτυξη στη διπλή μορφές, ευθείες δοκούς.

Μπορούμε να εξετάσει σε αυτή τη μελέτη μια σειρά από βασικές ερωτήσεις που θα βοηθήσουν στην καθοδήγηση της ανάπτυξης:

• Πώς ορίζουμε δύο προβολικές?
• Πόσα ομόλογα στοιχεία είναι απαραίτητο να καθοριστεί μια προβολικότητα
• Πώς μπορούμε να αποκτήσουμε ομόλογων στοιχείων από το δεδομένο?

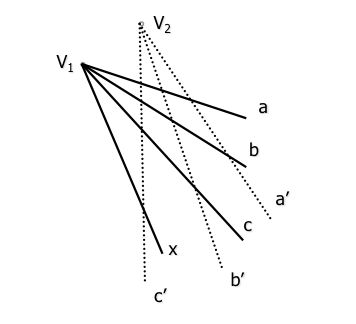
Οι δύο προβολικές δέσμες αποφασισμένοι να προσδιορίσουμε τρία ζεύγη ομόλογων ευθεία (α-α ', Β-Β ', C-C '), που βρίσκεται στις αντίστοιχες βάσεις τους (κατάγονται από τις αντίστοιχες κορυφές τους).

Ένα τέταρτο στοιχείο κορυφή δοκού x “V1” διαθέτει μία νέα ray x’ δέσμη ομόλογο (προβολικές) de base (κορυφή) “V1”” έτσι ώστε η εγκάρσια αναλογία quaternions διατηρείται προσδιορισμό:

(abcx) = (a'b'c'x »)

Για τον προσδιορισμό του ομολόγου του x θα λειτουργεί χρησιμοποιώντας το ενδιάμεσο μεταξύ των συνόλων που σχετίζονται perspectividades (χωρισμένο) στοιχεία και των δύο δοκών.

Στη μελέτη η θεώρηση γεγονότων είδαμε ότι η σειρά των προοπτικών (κέντρο προοπτική με μια κοινή hazproyección κορυφή), έχουν ένα διπλό σημείο που περιέχεται στη βάση (τομής των ευθειών παρένθεση) σειρά.

Στο σχήμα το διπλό σημείο είναι D = D’ περιέχουν μια ευθεία R και R’ σειρά perspectival perspectival κεντρικό σημείο με V.

Αυτή η ιδιότητα είναι σημαντική για την εύρεση της σειράς προοπτικές που συνδέει τις δύο προβολικές δέσμες που σημαίνει απλοποιημένη επεξεργασία, όπως συζητείται κατωτέρω.

Δεδομένων δύο προβολικές δέσμες ελεύθερα V1 και V2, προχωρήσει να τους κοπεί από δύο γραμμές r και r’ τον καθορισμό της σειράς με τις προοπτικές που κάνουν. Ανάμεσα στα αμέτρητα ζευγάρια των γραμμών που μπορούμε να χρησιμοποιήσουμε για να διακόψει αυτές τις δέσμες, επιλέξουν δύο διέρχεται από οποιοδήποτε σημείο της τομής των δύο ομόλογες στοιχείων των δοκών. Το σημείο D = D’ περιέχει το ζεύγος d-d’ αυτών των δοκών.

Αυτά τα σύνολα σημείων των βάσεων R και R 'είναι perspectival καθένα από τα οποία διπλού σημείου D = D '

Το σημείο CP είναι η προοπτική της σειράς de βάσεις r και r ' ότι το τμήμα της δέσμης των ακτίνων. Μεταβάλλοντας οποιαδήποτε από τις βάσεις της σειράς (r o r ') στο τμήμα D-D ', αυτή η σειρά θα συνεχίσει να είναι οι προοπτικές (έχοντας ένα διπλό σημείο) αλλά η προοπτική αλλάζει από τη μεσαία θέση. Αν και η αλλαγή του κέντρου, κατασκευή για τον προσδιορισμό των ομόλογων στοιχεία εξακολουθούν να ισχύουν και.

Προβολική Κέντρο

Χρησιμοποιώντας δύο ομόλογες ακτίνες ως βάσεις της σειράς r και r', Πρόκειται για προοπτικές για να έχουν ένα διπλό στοιχείο. Είμαστε στην πρώτη περίπτωση, δεδομένου ότι οι βάσεις διέρχεται από ένα σημείο (D-D ') Περιέχει δύο στοιχεία ομόλογο, αλλά στην περίπτωση αυτή την προοπτική σειρά κέντρο είναι μοναδική και δεν εξαρτάται από το ζευγάρι των ακτίνων που εκλέγονται για τη δημιουργία σειράς προοπτικές. Αν κοπεί επομένως από ένα-ένα.’ ή β-β’ … η προοπτική είναι το ίδιο, και θα επικοινωνήσουμε μαζί σας “προβολική κέντρο των δοκών“

Το Cp είναι το Κέντρο προοπτική σειρά Βάση r και r', είναι με τη σειρά του προβολική κέντρο των δοκών de βάσεις V1 και V2

Ακτίνες m = n’ η προβολή των δύο βάσεων (ευθεία V1-V2) έχουν peer της προβολής από το κέντρο των αντίστοιχων βάσεων.

Θα δούμε αργότερα πώς να χρησιμοποιήσει το προβολική κέντρο να καθορίσει ζεύγη ομόλογων στοιχεία των δοκών.

Προβολική Γεωμετρία