Τα Κωνικά ως Τόπος Κέντρων Εφαπτομένων Κύκλων

Hemos visto que el estudio de las cónicas se puede realizar desde diferentes enfoques geométricos.

Ειδικότερα, al iniciar el análisis de las cónicas hemos definido la elipse como lugar geométrico, είπαμε ότι:

La Elipse es el lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos, denominados Focos, tiene un valor constante.

Esta definición métrica de esta importante curva nos permite abordar su estudio relacionándolo con el de las circunferencias tangentes, conocido como el “Απολλώνιο πρόβλημα” en alguna de sus versiones. Cuando abordemos el estudio de las parábola o de la hipérbola volveremos a replantear el problema para generalizar estos conceptos y reducir los problemas al “Problema fundamental de tangencias en el caso recta“, ή το “Problema fundamental de tangencias en el caso circunferencia“, δηλαδή, la determinación de una circunferencia de un “Haz corradical” con una condición de tangencia.

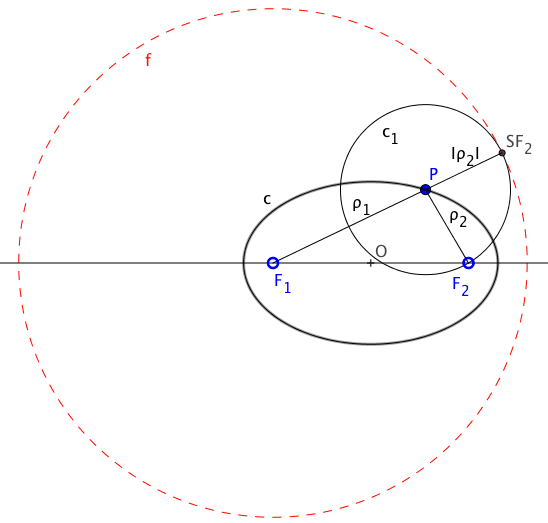
Supongamos, aplicando la definición anterior de la elipse, que los puntos fijos son F1 και F2. Estos puntos son los focos de la elipse. Supongamos además que la cónica se termina de definir por la condición de paso por un punto dado P.

Según la definición anterior la suma de distancias desde P a los dos focos debe ser constante. Llamaremos a esa suma “2ένα”.

ρ1 + ρ2 = 2a = constante

Si llevamos el segmento ρ2 a continuación del punto P según la dirección del segmento ρ1, obtendremos un punto “SF2” que dista del foco F1 el valor “2ένα“.

Al obtener todos los puntos de la cónica, como la suma de distancias a los focos es “2ένα“, los puntos similares al “SF2” se encontrarán a esa distancia (2ένα) del foco F1, por lo que se encontrarán en una circunferencia denominada “Circunferencia focal de la elipse“.

La circunferencia focal de una cónica es aquella circunferencia que tiene su centro en uno de sus focos y su radio es igual a la distancia entre los vértices de la cónica (2ένα)

Como la distancia del punto P al foco F2 que no es centro de la focal, es la misma que al punto “SF2”, la circunferencia que tiene su centro en el punto P y radio el valor “ρ2” θα περάσει “SF2” punto de la circunferencia focal, pero como además los centros “F1” de la focal y “P” de esta nueva circunferencia se encuentran alineados con el punto común de ambas “SF2”, este punto es de tangencia entre las dos circunferencias, lo que nos permite concluir que:

Los puntos de una elipse son los centros de las circunferencias que siendo tangentes a la circunferencia focal, pasan por el otro foco.

Esta definición de la cónica nos permite abordar los problemas de determinación de tangentes y puntos de paso o tangencia a la cónica mediante la solución de problemas de tangencias.

Για παράδειγμα, determinar los puntos de intersección de una recta con una cónica es determinar las circunferencias que tienen su centro sobre la recta, pasan por un foco y son tangentes a la circunferencia focal. Al tener su centro sobre la recta y pasar por un foco, pasarán por el simétrico de dicho foco respecto de la recta y el problema se reducirá a buscar circunferencias que pasando por dos puntos (foco y simétrico) son tangentes a la focal, δηλαδή, dos puntos de paso (pertenencia a un haz elíptico) y una condición de tangencia respecto de la circunferencia focal: Θεμελιώδες πρόβλημα της εφαπτόμενες.

Igual que obtenemos los puntos de una recta podemos relacionar las tangentes y los puntos de tangencia como se aprecia en la siguiente figura. Al ser la recta “r” tangente a la cónica, se puede deducir que es “la bisectriz” de los radios focales ρ1 και ρ2, como veremos más adelante.

¿Serías capaz de deducirlo tú?

Metric γεωμετρία