사영 기하학: 두 투영 번들 투영 센터

사영 모델 이원성의 법칙을 사용하면 다른 이전에 공제의 속성 및 듀얼 정리 세트를 얻을 수 있습니다. 사영 케이스 시리즈의 동종 요소를 획득하는 것은 perspectival 허용 중간 pespectividades를 획득하여 수행 한 우리는 우리라는 것을받을 수 있나요 “투영 축”. 우리는 사영 번들의 경우 그 볼, 듀얼 이유는 사영 센터를 결정하기 위해 우리를 이끌고.

El “세계” 포인트는 didactically 바로 듀얼보다 더 저렴, 그래서 우리를 위해 직선 시리즈와 관련된 개념과 분석을 시작했습니다, 지금, 이중 형태로 개발을 수행, 직선 빔.

우리는이 연구에서 개발을 안내하는 데 도움을 줄 것입니다 기본 일련의 질문을 고려할 수:

• 우리가 어떻게 두 개의 투영을 정의합니까?
• 상동 요소 projectivity를 결정할 필요가 얼마나 있는지
• 우리는 어떻게 부여에서 동종 요소를 얻을 수 있습니다?

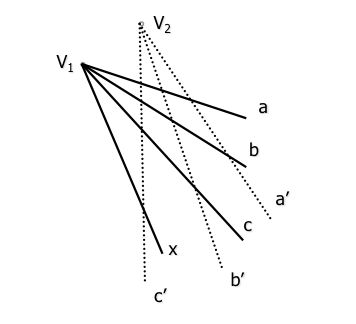
두 개의 투영 번들은 동종 바로 세 쌍을 정의하는 결정 (A-A ', 'B-B, C-C '), 각각의 기지에있는 (각각의 정점에있는 원래).

네 번째 요소 빔 정점 X “V1” 하나의 새로운 선 X를 가진다’ 상동 빔 (사영) 드베이스 (꼭지점) “V1”” 원수의 상호 비율을 결정 유지되도록:

(abcx) = (a'b'c'x ')

X의 상 동성을 결정하는 것은 perspectividades 연관 세트 사이의 중간을 사용하여 작동합니다 (단면) 두 빔의 요소.

공부에 perspectivity는 우리는 관점의 시리즈를 보았다 (공통의 정점 hazproyección 관점 센터), 베이스에 포함 된 두 지점이 (직선 브래킷의 교차) 시리즈.

그림에서 두 점은 D = D입니다’ 스트레이트 R 및 R을 포함’ V와 perspectival perspectival 중심점 시리즈.

이 속성은 간단한 치료를 의미하는 두 개의 투영 번들을 연결하는 전망 시리즈를 찾는 것이 필수적입니다, 아래에 설명 된대로.

Dados dos haces proyectivos de bases V1 과 V2, 두 줄의 R 및 R하여 그들을 잘라 진행’ 하고있는 그 잠재 시리즈를 결정. 우리는 이러한 빔을 절단하는 데 사용할 수있는 라인의 수많은 쌍 중, 빔의 두 동종 요소의 교차점의 지점을 통해 두 개의 패스를 선택. 점 D = D’ 쌍을 포함 d-d’ 이러한 빔.

Estas series de puntos de bases R 및 R '는 아르 perspectival 각되는 더블 포인트 D = D '

포인트 Cp es el centro perspectivo de las series 드 기지 R 과 R ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, 동종 요소의 결정에 대한 구조는 동일하게 유효.

Centro proyectivo

Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“

El punto Cp es el centro perspectivo de las series de bases r y r’, 차례로되는 centro proyectivo de los haces 드 기지 V1 y V2

Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.

Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.

사영 기하학