Intersezioni a Outlook: dritto e parallelepipedi

Uno dei problemi dei classici sistemi di rappresentazione è trovare l'intersezione di due elementi, ad esempio per determinare il punto di intersezione tra una linea e un piano. Natura topologica sono problemi in cui prevalgono i concetti di appartenenza.

I problemi sono basati su relazioni topologiche sono tipo di proiezione indipendenti in cui sono.

Problemi di intersezione sono basati sulla determinazione degli elementi geometrici che appartengono a due elementi simultaneamente, Considerando che questi sono formati da infiniti punti.

Studieremo l'esempio studiare il seguente problema:

Trova tutti i punti di intersezione della linea con il prisma r data in prospettiva cavalier, indicando la visibilità del rettilineo. Per risolvere questo problema nel precedentemente ricordate problemi di incidenza, determinare il punto di intersezione tra una linea e un piano.
Abbiamo visto il modello generale per la determinazione sistemi intersezioni rappresentazione. In questo approccio, avere un piano ausiliario contenente la linea data e Vi produrre una linea retta interseca il piano.

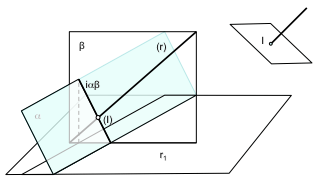
In questo tipo di problemi, quando l'intersezione è un prisma, abbiamo costantemente ripetiamo il problema di intersezione tra i piani. Per esempio possiamo risolvere in prima istanza intersezione di una retta r con un cuboide (una scatola con facce parallele e perpendicolari tra loro). La linea sarà determinata da una proiezione diretta (r) e la proiezione sul piano della base (r1)

Questo determinerà ad un piano contenente la linea, in questo caso, è ortogonale alla base. Ciò produrrà un piano retta interseca con il corpo che contiene i punti di intersezione.

• Determinare intersezione di queste linee si baserà sulle condizioni di parallelismo tra i diversi piani del corpo, da un piano sezionata due piani paralleli come linee parallele.
• Se il piano è perpendicolare alla base, intersezione con altri piani perpendicolari a queste linee verticali determinare.

Se il corpo è più complessa risolviamo intersezioni con alcuni lavori di più, anche se il modello generale è lo stesso se le facce rimangono parallelo alla proiezione.

Per risolvere questo esercizio, determinato prima sezione che provoca il piano contenente la retta RYA sua proiezione sul piano orizzontale XY (r1), sul corpo prismatico come. I punti di entrata e di uscita (1, 2, 3, 4, 5 e 6) sono ottenuti come punti di intersezione della linea con detta sezione r.

Vedremo più avanti come risolvere i casi in cui SLOPED facce.

Sistemas_de_representacion