 O estudo da cónica pode ser feita a partir de diferentes abordagens geométricas. Um dos mais utilizados que a análise é determinada a partir de seções planas em um cone de revolução.
O estudo da cónica pode ser feita a partir de diferentes abordagens geométricas. Um dos mais utilizados que a análise é determinada a partir de seções planas em um cone de revolução.
A partir desta definição, é possível inferir propriedades métrica destas curvas, além de novas definições da mesma.
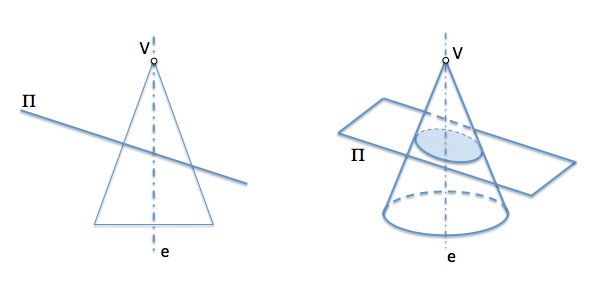
Usamos para analisar o caso em que o resultado da curva em secção plana de um cone de revolução é uma elipse. Neste caso, o ângulo formado pelo plano da secção com o eixo do cone foi maior do que o ângulo superior a metade.
Subsequentemente semelhante pode analisar os casos em que a curva é uma parábola ou hipérbole.
É, portanto, um ápice do cone revolução “V” e eixo “e”, Tem sido seccionado ao longo de um plano que passa pela sua não ápice. Este plano determina uma curva é uma elipse assumirá para o nosso estudo.
Se considerarmos um plano tangente à esfera e, simultaneamente, a superfície cónica, com o seu centro de modo a que o eixo geometricamente. Esta área vai entrar em contato com a circunferência do cone “c” contido num plano perpendicular ao seu eixo “e”. A intersecção deste plano com a seção de produzir é uma diretriz linha denominate “d” círio.
No ponto de contato entre a esfera e o plano que contém a curva vamos chamá-lo “Foco círio”.
ponto estreitamento localizado no plano de simetria irá denominar assembly “vértice círio”
No caso da elipse, que pode determinar uma segunda esfera, por isso esta curva tem dois vértices, dos focos y dos directrices.
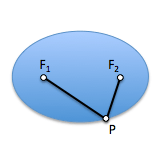
Si consideramos un punto “P” cualquiera de la curva y las distancias desde este punto a los focos de la elipse, PF1 e PF2, podemos determinar una propiedad métrica de esta curva que nos dará paso a una definición muy útil de la misma.
Como las tangentes desde un punto P a una esfera tienen igual longitud, se cumplirá que las tangentes desde P a la primera esfera, PF1 y PM, miden lo mismo. De igual forma ocurrirá con las tangentes desde este punto a la segunda esfera, PF2 y PN.
Por ello podemos determinar que la suma de estas dos distancias, PF1 y PF2, es igual a la distancia MN sobre la generatriz del cono limitada por los planos que contienen a las circunferencias de contacto c1 y c2.
Esto nos permite dar una definición de la elipse como la siguiente:
Elipse é o lugar geométrico dos pontos num plano cuja soma das distâncias a partir de dois pontos fixos, chamados Focos, Ele tem um valor constante.
Si consideramos a los vértices de la cónica como puntos de este lugar geométrico es fácil demostrar que la distancia de un foco a un vértice es igual a la distancia del otro foco al otro vértice y, con ello, demostrar que la suma de las distancias de un punto de la elipse a los focos es igual a la distancia entre los vértices de la cónica.






Deve estar conectado postar um comentário.