Conica definita dai due fuochi e tangente

Hemos resuelto la determinación de una cónica definida por sus dos focos y un punto mediante la circunferencia focal della conica.

Un problema utilizzando concetti identici sta determinando una nota conica suoi fuochi e loro tangenti. Vedremo questo problema, nel caso di un ellisse.

Supongamos que los datos son los focos de una elipse, F1 e F2, y una cualquiera de sus tangentes, t in figura.

El simétrico de uno de los focos respecto de la tangente debe encontrarse sobre la circunferencia focal de centro el otro foco.

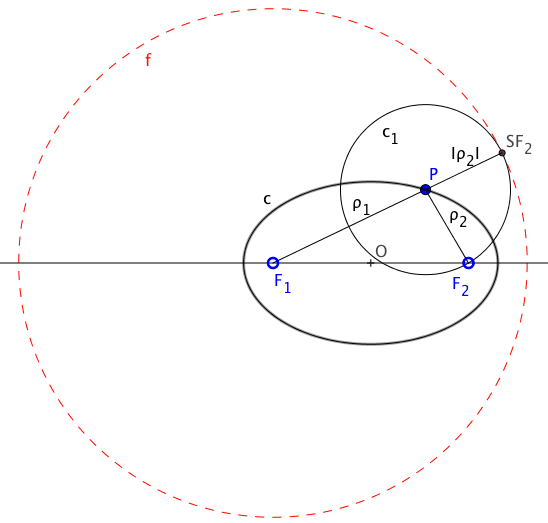
Como la tangente es bisectriz de los radios focales, podemos determinar el punto de tangencia

Para determinar los vértices podemos apoyarnos en el valor del radio de la circunferencia focal, 2un, ya que es la suma, costante, de los dos radios focales de cada punto de la cónica, tal y como vimos en la definición como lugar geométrico de circunferencias tangentes a la focal que pasaban por un punto dado.

Definizione della conica come locus di centri di circonferenza

In questo caso, se il punto di attraversamento è quello della tangenza T, la distanza da questo punto alla messa a fuoco che non è il centro della focale (F2) è uguale alla distanza dalla circonferenza focale (SF2). Il punto T sarà nel raggio della circonferenza focale che passa attraverso la simmetrica dell'altro fuoco rispetto alla tangente.

La conica è definita dai suoi elementi principali quando sono noti focolai e vertici.

E se invece di uno dei fuochi avessimo altre due tangenti? Sapresti come trovare l'altro focus?

Il problema sarebbe determinare la conica definita da un focus e tre tangenti.

GEOMETRÍA MÉTRICA