Las proyecciones principales de la recta sobre dos planos diédricos (수평 및 수직 평면) 새로운 비행기에 다른 직교 투영을 확인할 수 있도록.
우리는 일반적으로 2에서 새로운 투영을 확인 하는 방법을 볼 것 이다. Más adelante analizaremos su aplicación al estudiar las denominadas “proyecciones auxiliares”, incidiendo en su utilidad en la resolución de diferentes problemas.
En particular se suele utilizar frecuentemente la denominada “tercera proyección” que se realiza sobre un plano ortogonal a los anteriores denominado plano de perfil. Los tres planos ( 수평, H, Vertical, 에 y Perfil, 피) determinan un triedro trirrectángulo, en el que se tienen las tres coordenadas (엑스,과,부터) que permiten restituir la información espacial que tengamos representada (proyectada).
Al proyectar sobre un plano, la única coordenada que no se tiene proyectada en esta proyección es la perpendicular a dicho plano.
Si proyectamos sobre el plano horizontal (XY) la coordenada Z la tendremos sobre la proyección vertical, pero también sobre la correspondiente al plano de perfil.
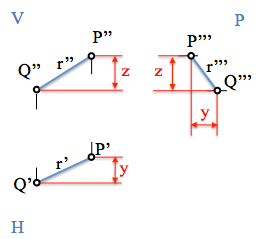
Vemos que dos planos ortogonales comparten una misma coordenada que puede servir para obtener la nueva proyección.
Dadas dos proyecciones sobre planos ortogonales : ¿Cómo podemos obtener la tercera proyección?
Para iniciar la representación que queremos obtener fijaremos un primer punto, P o Q, en la tercera proyección. El otro punto lo fijaremos mediante las cotas relativas que deben mantenerse.
Hemos visto que las proyecciones están vinculadas mediante líneas de referencia. Las nuevas proyecciones, 피”’ 과 큐”’ 똑바로, en tercera proyección, se encontrarán en las correspondientes líneas de referencia, por lo que mantendrán una misma “부터” o cota respecto del plano horizontal.
A su vez, el valor del “alejamiento”, coordenada “과“, respecto del plano vertical, 에, se mantiene en la tercera proyección, permitiendo por lo tanto la determinación de los puntos buscados.
Sistemas_de_representacion
반드시 연결된 댓글을 달다.