평면에 수직

우리는 표현 시스템을 연구함으로써 배울 기본적인 문제점 중 하나는 서로 수직 인 요소가있는 것들이다: Recta perpendicular a plano o a recta y plano perpendicular a otro plano. Todos los problemas de determinación de distancias hacen uso de los conceptos de ortogonalidad que desarrollaremos a continuación.

Separaremos en general el problema de determinación de la dirección normal a un plano o a rectas del establecimiento de su posición. Podemos hacer pasar una recta perpendicular por lo tanto por cualquier punto del espacio ya que en un primer acercamiento a este problema sólo nos interesa la orientación de dicha recta.

평면에 수직

Veamos cómo determinar la recta perpendicular a un plano en Sistema Diédrico trabajando directamente en las proyecciones principales del sistema. También podremos resolver mediante proyecciones auxiliares, 이 경우 연구 대상은 아니지만.

우리는 평면에 수직인 선을 찾는 데 필요한 공간 정리를 기억할 것입니다.:

평면에서 서로 평행하지 않은 두 직선에 수직인 경우 직선이 평면에 수직입니다..

평면에 수직인 선을 결정하기 위해 우리는 선이 다음과 같은 경우를 찾을 것입니다., 평면의 모든 선에 수직, 알려진 그들 중 하나에 수직으로 투영됩니다..

공부에 최대 라인 대기 중 비행기의, 적용 세 개의 수직 정리 , 우리는 그것이 투영 평면과의 교차점에 평행한 선에 수직으로 투영되는 것을 보았습니다..

물론, 이 줄 “lmp” 그것을 포함하는 평면과 투영면의 직선 교차점에 수직인 평면 A-A'-I에 위치합니다., 이 경우, 수평 “시간”. 일반적으로 선에 수직인 선 “시간” 그들은 수평면에 대한 투영에 수직인 선으로 투영됩니다.:

투영면에 평행한 선에 수직인 선은 이 투영면에서 해당 선에 수직으로 투영됩니다..

평면에 대한 법선은 평면의 수평선에 수직입니다., 모든 라인에 적용되기 때문에. 또한 최대 경사선에 수직이 됩니다. “lmp”. 이 선의 수평 투영은 투영 평면에 평행한 선이기 때문에 수평선의 투영에 수직이 됩니다..

물론, la recta “N” 평면에 수직인 평면은 투영 평면에 대해 최대 경사선을 포함하는 투영 평면에 있습니다., 그래서 이 평면에 대한 그것의 투영은 그것과 일치할 것이고 따라서 그것은 수평면에 수직이 될 것입니다..

따라서 법선을 결정하기 위해 수평 투영에서 방향을 결정할 수 있음을 알 수 있습니다., 가로와 수직이기 때문에. 유사한 추론으로 우리는 수직 투영에서 이 투영 평면에 평행한 평면의 선에 수직이 될 것이라고 결론을 내릴 수 있습니다. (최전선).

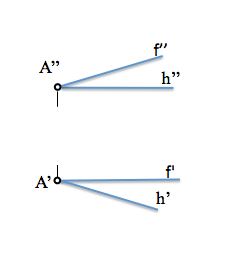
평면이 수평으로 정의된다고 가정합니다. “시간” 그리고 앞 “에프”.

La dirección normal al plano se puede determinar por las condiciones de ortogonalidad respecto de las rectas notables del plano, horizontal y frontal, tal y como hemos visto. Al existir infinitas rectas perpendiculares a un plano, una por cada uno de sus puntos, buscaremos una cualquiera para la determinación de su dirección.

Vemos que es necesario contar con las proyecciones de las rectas notables citadas (horizontales y frontales) para determinar la dirección normal a un plano. En un caso general no las tendremos ya que el plano puede ser definido de muy variadas formas: tres puntos, punto y recta, dos rectas, condiciones angulares o de paralelismo y puntos de paso ….

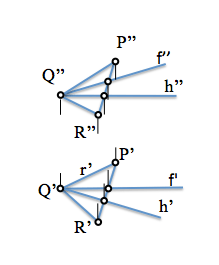
Podemos determinar las rectas paralelas a los planos de proyección que necesitemos. 이 경우 우리는 모든 평면의 수평과 최전선을 얻을 것입니다. (수직에 평행). 그림에서 우리는 점을 통과하는 것을 결정했습니다. “큐” 콘크리트.