 Para representar un objeto en el sistema diédrico normalmente usaremos la proyecciones sobre los tres planos del triedro de referencia, tal y como hemos visto al estudiar los fundamentos del sistema diédrico.
Para representar un objeto en el sistema diédrico normalmente usaremos la proyecciones sobre los tres planos del triedro de referencia, tal y como hemos visto al estudiar los fundamentos del sistema diédrico.
En general será suficiente con utilizar únicamente dos de los tres posibles planos, quedando representada por ejemplo una recta mediante sus proyecciones sobre el plano horizontal y el vertical. En ocasiones puede ser conveniente, o incluso necesario, obtener nuevas proyecciones según diferentes direcciones de proyección, en cuyo caso las llamaramos “proyecciones auxiliares” .
Supongamos que queremos obtener un nuevo plano de proyección que sustituya al plano vertical. Vemos que cualquier plano perpendicular al plano horizontal, como son el vertical y el de perfil, comparten la dirección normal a este plano y en consecuencia la coordenada “부터”,
Si definimos un nuevo plano vertical “V1” también compartirá esta coordenada “부터” que será necesaria para obtener la proyección auxiliar.
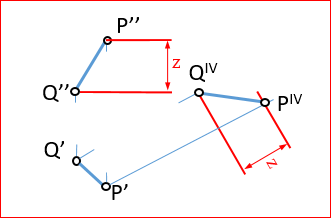
Supongamos que tenemos las proyecciones diédricas de una recta sobre sus planos horizontal y vertical.
Al realizar un nuevo plano vertical, como se ha visto, se conservará la coordenada “부터” relativa entre cada pareja de puntos de la proyección. Podemos determinar las coordenadas relativas de los puntos de la recta según esta dirección.
Supongamos que la nueva proyección está definida de forma que el punto “큐” se proyecta según “QIV” (proyección cuarta del punto Q)
Obtendremos las nuevas proyecciones de los puntos ya que se situarán sobre sus respectivas líneas de referencia con la proyección previa (en este caso la primera proyección o proyección horizontal) y además se conservarán las cotas relativas sobre el nuevo plano de proyección (en este caso la “부터”).
Para completar el estudio sólo falta determinar la mejor dirección para realizar la proyección auxiliar. Veremos cómo elegir esta dirección para poder situar los elementos paralelos o perpendiculares a las nuevas proyecciones, simplificando problemas de medida lineal o angular entre rectas y planos.








반드시 연결된 댓글을 달다.