 Resolvemos a determinação de um cônica definida por seus dois focos e um ponto por meio do circunferência focal círio.
Resolvemos a determinação de um cônica definida por seus dois focos e um ponto por meio do circunferência focal círio.
Um problema usando conceitos idênticos é determinar um conhecido cônica seus focos e suas tangentes. Veremos esse problema no caso de uma elipse.
Suponha que os dados sejam os focos de uma elipse, F1 e F2, e qualquer uma de suas tangentes, t na figura.
A simetria de um dos focos em relação à tangente deve estar na circunferência focal do centro do outro foco..
Como as bissetrizes tangentes os raios focais, podemos determinar o ponto de tangência
Para determinar os vértices podemos contar com o valor do raio da circunferência focal, 2a, pois é a soma, constante, dos dois raios focais de cada ponto da cônica, como vimos no definição como lugar geométrico das circunferências tangentes ao ponto focal que passa por um ponto dado.
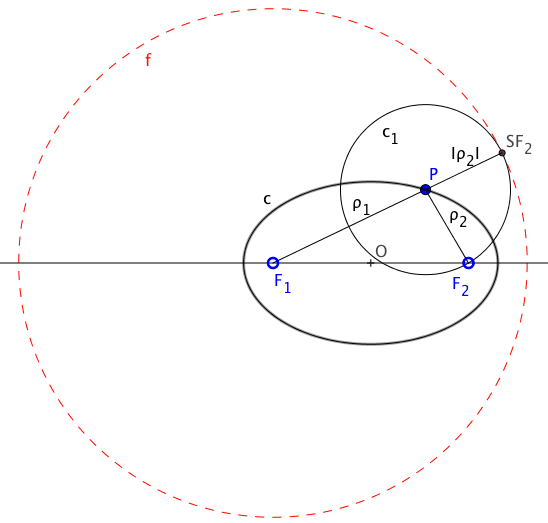
Neste caso, se o ponto de passagem é o ponto de tangência T, a distância deste ponto ao foco que não é o centro do foco (F2) é igual à distância ao círculo focal (SF2). O ponto T será encontrado no raio da circunferência focal que passa pela simetria do outro foco em relação à tangente.
A cônica é definida por seus elementos principais quando os focos e vértices são conhecidos.
E se em vez de um dos focos tivéssemos mais duas tangentes?? Você saberia como encontrar o outro foco?
O problema seria determinar a cônica que é definida por um foco e três tangentes.







Deve estar conectado postar um comentário.