Используя законы двойственности в проективных моделей могут получить набор свойств и Двойственные теоремы из других ранее вычитаются. Получение гомологичные элементы в проективной серии случаев была выполнена путем получения промежуточных pespectividades разрешенные перспективное мы получаем то, что мы назвали “Ось проективные”. Мы увидим, что в случае проективных пучков, Двойной рассуждения приводят нас к определить проективные центры.
El “мир” точки является более доступным, чем назидательно прямо двойного, поэтому мы начали анализ с понятий, связанных с прямолинейным серии для, сейчас, осуществлять развитие в дуальных форм, прямые лучи.
Мы можем рассмотреть в этом исследовании ряд основных вопросов, которые помогут направить развитие:
- Как мы определяем двух проективных?
- Сколько гомологичные элементы необходимы для определения проективность
- Как мы можем получить гомологичные элементы из дали?
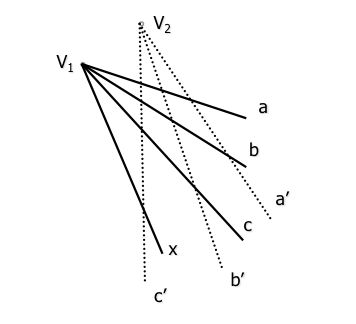
Два проективные расслоения определяются определить три пары гомологичной прямой (-', б-б ', С-С '), расположены на своих соответствующих базах (происходящих в их соответствующих вершин).
Четвертый элемент луча вершина х “V1” имеет один новый луч х’ гомолог луч (проективный) де база (вершина) “V1”” так что поперечное соотношение кватернионов сохраняется определения:
(ABCX) = (a'b'c'x ')
Для определения гомолог х будет работать с использованием промежуточного между подходами, которые относятся perspectividades (секционного) элементы обоих пучков.
При изучении перспективность Мы видели, что ряд точек зрения (перспектива центр с общей вершиной hazproyección), есть двойная точка, которая содержится в базе (Пересечение прямых скобках) серия.
На рисунке двойной Дело в том, D = D’ содержащую пр г и г’ серия перспективного перспективного центральной точки с V.
Это свойство очень важно для нахождения перспективы серию соединяющий две проективные расслоения что означает упрощенный режим, как описано ниже.
Dados dos haces proyectivos de bases V1 год V2, перейти, чтобы сократить их на две линии г и г’ определения серию с теми перспективами, которые делают. Среди бесчисленных пар линий, что мы можем использовать, чтобы разорвать эти лучи, выбрать два проходящий через точки пересечения двух гомологичных элементов балок. Дело в D = D’ содержит пару d-d’ из этих лучей.
Estas series de puntos de bases г и г 'являются перспективное каждый из которых двойная точка D = D '
Точка Cp es el centro perspectivo de las series де базы R год г ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, строительство для определения гомологичных элементов остаются одинаковую юридическую силу.
Проективная центр
Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“
El punto Cp es el centro perspectivo de las series de bases r y r’, будучи в свою очередь centro proyectivo de los haces де базы V1 y V2
Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.
Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.
GEOMETRIA Proyectiva
Должно быть связано добавить комментарий.