 Uno de los problemas básicos que debemos aprender al estudiar los Sistemas de Representación son aquellos en los que aparecen elementos que son perpendiculares a otros: Recta perpendicular a plano o a recta y plano perpendicular a otro plano. Todos los problemas de determinación de distancias hacen uso de los conceptos de ortogonalidad que desarrollaremos a continuación.
Uno de los problemas básicos que debemos aprender al estudiar los Sistemas de Representación son aquellos en los que aparecen elementos que son perpendiculares a otros: Recta perpendicular a plano o a recta y plano perpendicular a otro plano. Todos los problemas de determinación de distancias hacen uso de los conceptos de ortogonalidad que desarrollaremos a continuación.
Separaremos en general el problema de determinación de la dirección normal a un plano o a rectas del establecimiento de su posición. Podemos hacer pasar una recta perpendicular por lo tanto por cualquier punto del espacio ya que en un primer acercamiento a este problema sólo nos interesa la orientación de dicha recta.
Recta perpendicular a un plano
Veamos cómo determinar la recta perpendicular a un plano en Sistema Diédrico trabajando directamente en las proyecciones principales del sistema. También podremos resolver mediante proyecciones auxiliares, aunque no es el objeto del estudio en este caso.
Recordaremos un teorema espacial que será necesario para encontrar una recta perpendicular a un plano:
Una recta es perpendicular a un plano si lo es a dos rectas de dicho plano que no sean paralelas entre sí.
Para determinar una recta perpendicular a un plano buscaremos aquellos casos en que la recta, siendo perpendicular a todas las rectas del plano, se proyecte perpendicular a alguna de ellas que sean conocidas.
Al estudiar la línea de máxima pendiente de un plano, aplicando el teorema de las tres perpendiculares , vimos que ésta se proyectaba perpendicular a las rectas paralelas a su intersección con el plano de proyección.
En efecto, esta línea “lmp” se encuentra en el plano A-A’-I que es perpendicular a la recta intersección del plano que la contiene con el plano de proyección, en este caso la horizontal “h”. En general las rectas perpendiculares a la recta “h” se proyectarán como rectas perpendiculares a su proyección sobre el plano horizontal:
Toda recta perpendicular a una recta paralela a un plano de proyección se proyecta perpendicular a dicha recta en este plano de proyección.
La recta normal al plano será perpendicular a las horizontales del plano, ya que lo es a todas sus rectas. También será perpendicular a su línea de máxima pendiente “lmp”. La proyección horizontal de esta recta será perpendicular a la de las horizontales por ser rectas paralelas al plano de proyección.
En efecto, la recta “n” normal al plano se encuentra en un plano proyectante que contiene a la línea de máxima pendiente respecto del plano de proyección, por lo que su proyección sobre este plano coincidirá con ella y por lo tanto será perpendicular a las horizontales.
Vemos pues que para determinar la normal podemos determinar su dirección en la proyección horizontal, ya que es perpendicular a las horizontales. Con un razonamiento similar podemos concluir que en la proyección vertical será perpendicular a las rectas del plano que son paralelas a este plano de proyección (rectas frontales).
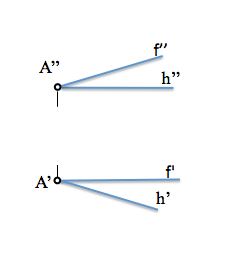
Supongamos que el plano queda definido mediante una horizontal “h” y una frontal “f”.
La dirección normal al plano se puede determinar por las condiciones de ortogonalidad respecto de las rectas notables del plano, horizontal y frontal, tal y como hemos visto. Al existir infinitas rectas perpendiculares a un plano, una por cada uno de sus puntos, buscaremos una cualquiera para la determinación de su dirección.
Vemos que es necesario contar con las proyecciones de las rectas notables citadas (horizontales y frontales) para determinar la dirección normal a un plano. En un caso general no las tendremos ya que el plano puede ser definido de muy variadas formas: tres puntos, punto y recta, dos rectas, condiciones angulares o de paralelismo y puntos de paso ….
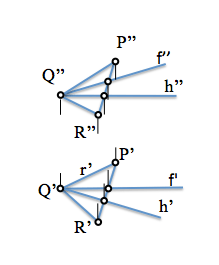
Podemos determinar las rectas paralelas a los planos de proyección que necesitemos. En este caso obtendremos una horizontal de plano cualquiera así como una recta frontal (paralela al vertical). En la figura se han determinado las que pasan por un punto “Q” concreto.
La obtención de la normal es inmediata tal y como ya hemos visto.
A partir de estos conceptos podemos plantear nuevos problemas como el de determinación de la distancia desde un punto a un plano. ¿Sabrías resolverlo?









Debe estar conectado para enviar un comentario.