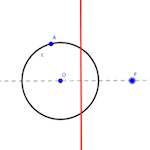
Inversión: Tabla de gimnasia mental para determinación de elementos con condiciones angulares
Ya hemos usado una “Tabla de Gimnasia Mental” al estudiar la inversión: un conjunto de ejercicios que sirven para estimular el razonamiento, desarrollar y mantener la mente ágil, automatizar procesos de cálculo y análisis etc.
Nos proponemos ahora plantear una serie similar de problemas pero encaminados a obtener soluciones a problemas básicos de geometría. En este caso plantearemos la búsqueda de circunferencias que pasen por un punto dado y cumplan condiciones angulares respecto de otras dos circunferencias.