Perpendicular to a plane

One of the basic problems that we learn by studying the systems of representation are those in which there are elements that are perpendicular to other: Recta perpendicular a plano o a recta y plano perpendicular a otro plano. Todos los problemas de determinación de distancias hacen uso de los conceptos de ortogonalidad que desarrollaremos a continuación.

Separaremos en general el problema de determinación de la dirección normal a un plano o a rectas del establecimiento de su posición. Podemos hacer pasar una recta perpendicular por lo tanto por cualquier punto del espacio ya que en un primer acercamiento a este problema sólo nos interesa la orientación de dicha recta.

Perpendicular to a plane

Veamos cómo determinar la recta perpendicular a un plano en Sistema Diédrico trabajando directamente en las proyecciones principales del sistema. También podremos resolver mediante proyecciones auxiliares, although not the subject of this case study.

Remember a spatial theorem it will be necessary to find a line perpendicular to a plane:

A straight line is perpendicular to a plane if it is two lines of said plane are not parallel to each other.

Determining a line perpendicular to a plane find cases where the line, It is perpendicular to all straight plane, is projected perpendicular to any of them that are known.

By studying the maximum line pending a plane, applying theorem of three perpendicular , We saw it projected perpendicular to lines parallel to its intersection with the projection plane.

Indeed, this line “lmp” It is in the plane A-A'-I that is perpendicular to the line intersection of the plane which contains the projection plane, in this case the horizontal “h”. In general lines perpendicular to the straight “h” They were screened as perpendicular to its projection on the horizontal plane:

Any line perpendicular to a line parallel to a projection plane is projected perpendicular to said straight projection in this plane.

The normal line to the plane will be perpendicular to the horizontal plane, since it is all straight. It will also be perpendicular to its fall line “lmp”. The horizontal projection of this line is perpendicular to the horizontal lines being parallel to the projection plane.

Indeed, The straight “n” normal to the plane is a projecting plane containing the line of maximum slope with respect to the projection plane, so that its projection on this plane coincide with it and thus is perpendicular to the horizontal.

We see that in determining normal we can determine its direction in the horizontal projection, as it is perpendicular to the horizontal. By similar reasoning we can conclude that in the vertical projection is perpendicular to the straight plane that are parallel to the projection plane (front straight).

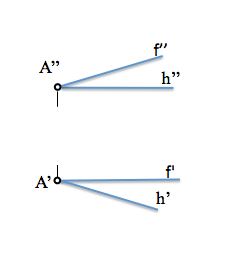
Suppose that the plane is defined by a horizontal “h” and a front “f”.

La dirección normal al plano se puede determinar por las condiciones de ortogonalidad respecto de las rectas notables del plano, horizontal y frontal, tal y como hemos visto. Al existir infinitas rectas perpendiculares a un plano, una por cada uno de sus puntos, buscaremos una cualquiera para la determinación de su dirección.

Vemos que es necesario contar con las proyecciones de las rectas notables citadas (horizontal and frontal) para determinar la dirección normal a un plano. En un caso general no las tendremos ya que el plano puede ser definido de muy variadas formas: three points, punto y recta, dos rectas, condiciones angulares o de paralelismo y puntos de paso ….

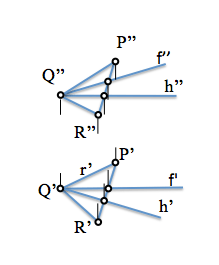
Podemos determinar las rectas paralelas a los planos de proyección que necesitemos. In this case we obtain a horizontal plane as well as any a front straight (parallel to the vertical). In figure they have been determined to pass a point “Q” concrete.