 우리는 원뿔형 연구가 다양한 기하학적 접근 방식으로 수행될 수 있음을 확인했습니다..
우리는 원뿔형 연구가 다양한 기하학적 접근 방식으로 수행될 수 있음을 확인했습니다..
특히, al iniciar el análisis de las cónicas hemos definido la elipse como lugar geométrico, 우리는 그렇게 말했다:
타원은 두 개의 고정된 점까지의 거리의 합이 있는 평면 점의 기하학적 자취입니다., Focus라고 불리는, 일정한 값을 갖는다.
이 중요한 곡선에 대한 미터법 정의를 통해 접선 원의 곡선과 관련시켜 연구에 접근할 수 있습니다., 로 알려진 “아폴로 니 오 스의 문제” 일부 버전에서는. 포물선이나 쌍곡선 연구에 접근할 때, 우리는 이러한 개념을 일반화하고 문제를 다음과 같이 축소하기 위해 문제를 다시 언급할 것입니다. “직선의 경우 접선의 근본적인 문제“, 또는 “원주 경우의 접선의 근본적인 문제“, 즉, 원주 결정 “위험 지역” 접선 조건이 있는 경우.
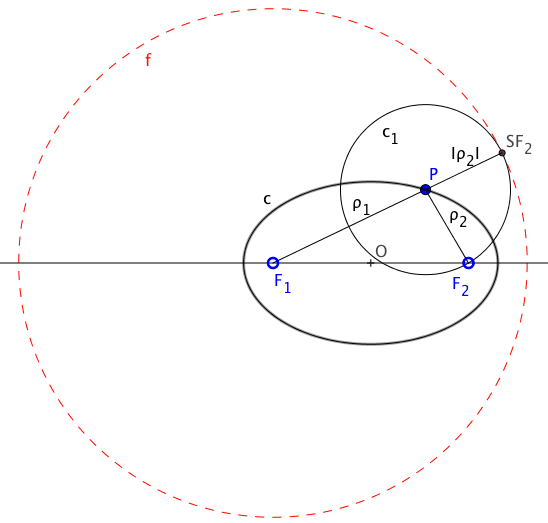
Supongamos, aplicando la definición anterior de la elipse, que los puntos fijos son F1 과 F2. Estos puntos son los focos de la elipse. Supongamos además que la cónica se termina de definir por la condición de paso por un punto dado 피.
Según la definición anterior la suma de distancias desde P a los dos focos debe ser constante. Llamaremos a esa suma “2a”.
ρ1 + ρ2 = 2a = constante
Si llevamos el segmento ρ2 a continuación del punto 피 según la dirección del segmento ρ1, obtendremos un punto “SF2” que dista del foco F1 el valor “2a“.
Al obtener todos los puntos de la cónica, como la suma de distancias a los focos es “2a“, los puntos similares al “SF2” se encontrarán a esa distancia (2a) del foco F1, por lo que se encontrarán en una circunferencia denominada “Circunferencia focal de la elipse“.
La circunferencia focal de una cónica es aquella circunferencia que tiene su centro en uno de sus focos y su radio es igual a la distancia entre los vértices de la cónica (2a)
Como la distancia del punto P al foco F2 que no es centro de la focal, es la misma que al punto “SF2”, 둘레 que tiene su centro en el punto P y radio el valor “ρ2” 에 의해 전달 됩니다. “SF2” punto de la circunferencia focal, pero como además los centros “F1” de la focal y “피” de esta nueva circunferencia se encuentran alineados con el punto común de ambas “SF2”, este punto es de tangencia entre las dos circunferencias, lo que nos permite concluir que:
Los puntos de una elipse son los centros de las circunferencias que siendo tangentes a la circunferencia focal, pasan por el otro foco.
Esta definición de la cónica nos permite abordar los problemas de determinación de tangentes y puntos de paso o tangencia a la cónica mediante la solución de problemas de tangencias.
예를 들면, determinar los puntos de intersección de una recta con una cónica es determinar las circunferencias que tienen su centro sobre la recta, pasan por un foco y son tangentes a la circunferencia focal. Al tener su centro sobre la recta y pasar por un foco, pasarán por el simétrico de dicho foco respecto de la recta y el problema se reducirá a buscar circunferencias que pasando por dos puntos (foco y simétrico) son tangentes a la focal, 즉, dos puntos de paso (pertenencia a un haz elíptico) 초점 원주에 대한 접선 상태: 접선의 근본적인 문제.
선의 점을 구하는 것처럼 다음 그림과 같이 접선과 접선점을 연관시킬 수 있습니다.. 이성애자 “R” 원뿔에 접하는, 것이라고 추론할 수 있다. “이등분선” 초점 반경 ρ1 과 ρ2, 아래에 논의된 바와 같이.
추론해 볼 수 있을까요??






반드시 연결된 댓글을 달다.