El estudio de las cónicas se puede realizar desde diferentes enfoques geométricos. Uno de las análisis más usado es el que las determina a partir de secciones planas en un cono de revolución.
A partir de esta definición es posible inferir propiedades métricas de estas curvas, además de nuevas definiciones de las mismas.
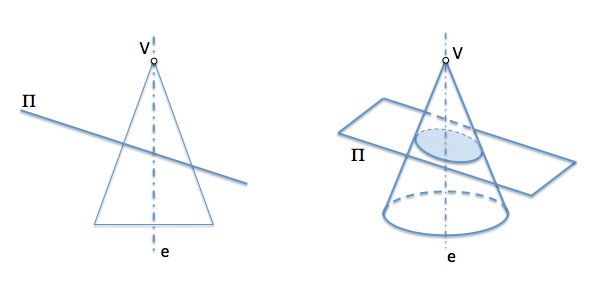
Utilizaremos para el análisis el caso en el que la curva resultado de la sección plana en un cono de revolución es una elipse. En este caso el ángulo que formaba el plano de la sección con el eje del cono era mayor que el semiángulo en el vértice.
Posteriormente se podrá analizar de forma similar los casos en los que la curva sea una parábola o una hipérbola.
Quindi sii un cono di rivoluzione dei vertici “In” e asse “e”, che è stato sezionato da un piano che non passa attraverso il suo vertice. Questo piano determina una curva che supponiamo sia un'ellisse per il nostro studio..
Se consideriamo una sfera tangente al piano e, contemporaneamente, alla superficie conica, con il suo centro quindi sull'asse di questa forma geometrica. Questa sfera avrà una circonferenza a contatto con il cono “c” contenuto in un piano perpendicolare al suo asse “e”. L'intersezione di questo piano con cui la sezione produce è una linea che chiameremo direttrice “d” della conica.
Chiameremo il punto di contatto tra la sfera e il piano che contiene la curva “fuoco della conica”.
Chiameremo il punto della conica che si trova sul piano di simmetria dell'insieme “vertice della conica”
Nel caso dell'ellisse possiamo determinare una seconda sfera, quindi questa curva avrà due vertici, due fuochi e due linee guida.
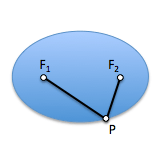
Se consideriamo un punto “P” qualsiasi curva e le distanze da questo punto ai fuochi dell'ellisse, PF1 e PF2, possiamo determinare una proprietà metrica di questa curva che ci darà una definizione molto utile di essa.
Poiché le tangenti da un punto P a una sfera hanno la stessa lunghezza, si adempirà a ciò tangenti da P alla prima sfera, PF1 e PM, misurano lo stesso. Allo stesso modo accadrà con le tangenti da questo punto alla seconda sfera, PF2 e PN.
Pertanto possiamo determinare che la somma di queste due distanze, PF1 e PF2, è uguale alla distanza MN sulla generatrice del cono limitata dai piani contenenti i cerchi di contatto c1 e c2.
Questo ci consente di dare una definizione dell'ellisse come la seguente:
Ellisse è il luogo dei punti in un piano la cui somma delle distanze da due punti fissi, chiamati Faretti, Ha un valore costante.
Se consideriamo i vertici della conica come punti di questo locus, è facile dimostrare che la distanza da un focus a un vertice è uguale alla distanza dall'altro focus all'altro vertice e, con esso, dimostralo la somma delle distanze da un punto dell'ellisse ai fuochi è uguale alla distanza tra i vertici della conica.
Deve essere collegato per pubblicare un commento.