 난 항상 내 학생들을 하나 개의 권장 사항은 다른 방식으로 같은 문제를 해결하는 것입니다, 거의 유사한 진술로 동일한 문제를 여러 번 수행하는 대신.
난 항상 내 학생들을 하나 개의 권장 사항은 다른 방식으로 같은 문제를 해결하는 것입니다, 거의 유사한 진술로 동일한 문제를 여러 번 수행하는 대신.
지난 수업 중 하나에서 우리는 점의 역함수를 얻는 것을 제안했습니다., 중심과 거듭제곱이 알려진 역전에서. 제안된 성명은 다음과 같았습니다:
그림의 제곱이 주어지면, 꼭지점 중 하나가 반전 중심이고 반대쪽 꼭지점이 이중 점인 경우, 점 A의 역수를 결정 (인접한 꼭지점).
우리는 두 가지 모두에서 사용되는 개념을 기반으로 하는 다양한 구성을 찾을 수 있습니다. 메트릭 형상 에는 사영 기하학. 처음에는 미터법 성격의 다섯 가지 솔루션으로 연구를 시작할 것입니다..
비행기에 투자
두 개의 역점 사이의 미터법 관계를 기억하는 것부터 시작하겠습니다., 의 장에서 공부했습니다. “비행기에 투자“.
- 투자는 센터를 통한 변화입니다. 각 포인트 A 그리고 그것은 변형되었습니다 A’ 투자센터와 연계되어 있습니다. 나는.
- 반전 중심에서 한 점까지의 거리와 그 변환의 곱이 일정하며 이를 반전력이라고 합니다.. IA*IA'=cte.
제안된 연습에서는, 이중점을 알 때, 대각선 제곱의 가치인 투자력을 우리는 알고 있습니다.. 중심이 투자이고 반지름이 거듭제곱의 근인 원의 모든 점입니다. (정사각형의 대각선) 포인트가 2배가 됩니다. 이 둘레는 다음과 같이 알려져 있습니다. “자기 반전 둘레”
1 Teorema del cateto
제안된 첫 번째 모델은 가장 많이 사용되는 정리 중 하나를 기반으로 했습니다. 메트릭 기하학, el “카테토의 정리”.
El 정리 다리 비례 평균을 사용하여 빗변에 투영된 직각삼각형의 다리와 그 곱을 연관시킬 수 있습니다..

Teorema del cateto

세그먼트 IT를 직각삼각형의 변으로 간주하고 세그먼트 IA를 이 변의 투영으로 간주하는 경우, T를 통해 수직을 얻음으로써 점 A를 얻습니다.’ AI가 되는 것’ 직각삼각형의 빗변.
2 Teorema del cateto
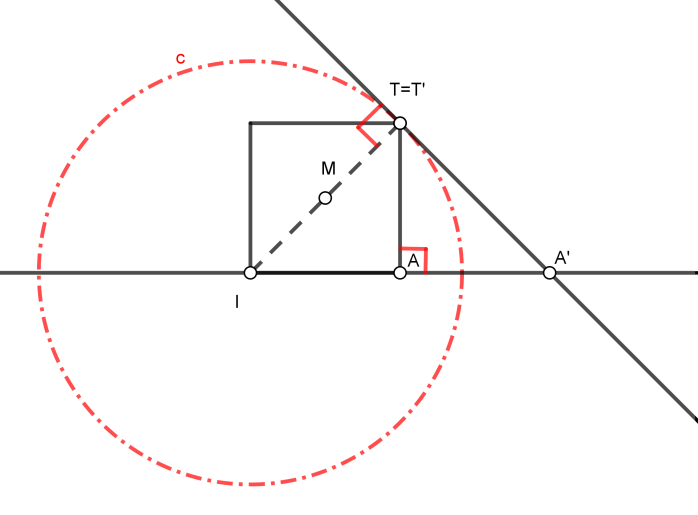
동일한 개념을 바탕으로 직각삼각형을 지지하는 90° 각도의 호를 결정하는 새로운 구성을 만들 수 있습니다.. 원하는 분절이 가능한 이 아치 IA’ 점을 통과하는 반원이므로 구하겠습니다. 나는 과 티, 그리고 그 중심은 직선 위에 있습니다 IA. 우리는 세그먼트의 이등분선을 결정합니다 그것 (que pasará por el punto A en este caso particular al ser la diagonal de un cuadrado) y de terminaremos el centro del arco capaz sobre la recta IA.
3 전원 개념
La potencia de un punto respecto de una circunferencia, que definimos como la mayor por la menor distancia del punto a dicha circunferencia y que es igual al segmento de tangencia (desde el punto a la circunferencia) al cuadrado, nos permite obtener nuevas construcciones.
En la figura vemos cómo el segmento de tangencia “l” es media proporcional entre “엠” 과 “N”.


Para la nueva construcción determinaremos una circunferencia en la que IT es el segmento de tangencia y debe pasar además por el punto “A“, por lo que su centro estará en la intersección de la recta perpendicular a “I-T” 로 “티“, con la mediatriz de “A-T”
4 전원 개념: Antiparalelismo
El concepto de potencia de un punto respecto de una circunferencia se basa en el producto de la mayor por la menor de las distancias de un punto a una circunferencia.
이러한 거리 값 원주와 포인트의 중심을 포함 하는 문자열에서 주어진 다, 즉, en el diámetro que contiene a dicho punto. Es posible generalizar este concepto para considerar otras cuerdas que pasen por el punto 피, como hemos visto en la “Generalización del concepto de potencia“.

적용 teorema de Thales a los dos triángulos semejantes (PAD y PCB ya que comparten el ángulo en P y por ángulos en la circunferencia, arco capaz, son iguales en B y D) obteníamos que:
PA/PD = PC/PB
y por lo tanto
PA * PB = PC * PD = Constante
Lo que demostraba que la potencia desde el punto P es independiente de la recta elegida, como queríamos demostrar.
선 AB와 CD는 AD와 CB와 역평행하며, 2x2로 같은 각도를 형성합니다..
우리의 경우 I-T-T 라인’ 그리고 I-A-A’ A-T와 역평행할 것이다’ y A'-T, 이 경우 직각은 2x2로 형성된 각도입니다..
5 직선 투자
도형을 반전시킬 때 반전 중심을 통과하지 않는 선의 역은 이 점을 통과하는 원이라는 것을 보았습니다., 그 중심은 투자 중심으로부터의 선과 수직이다.
역수 A-T 세그먼트 중심이 직선에 위치하는 원호가 됩니다. I-A, 투자센터를 통과하게 됩니다 “나는” 더블포인트 뿐만 아니라 “ㅜㅜ'”
Las 5 첫 번째 솔루션은 본질적으로 측정 기준입니다.. 우리는 다른 사람들을 볼 것입니다 5 다음 링크에서 투영 기하학의 개념을 사용합니다..
(이 링크에서 곧 만나보실 수 있습니다 ….) 점의 역수를 구하는 사영해









반드시 연결된 댓글을 달다.