 Mit den Gesetzen der Dualität in der projektiven Modelle können eine Reihe von Eigenschaften und Dual-Sätze aus der anderen zuvor abgezogen bekommen. Beziehen homologen Elemente in der projektiven Fallserie wurde durch den Erwerb Zwischen pespectividades erlaubt perspektivisch durchgeführt haben wir bekommen, was wir genannt haben “projektive Achse”. Wir werden, dass im Fall der projektiven Bündeln sehen, Dual-Argumentation führt uns zu projektiven Zentren bestimmen.
Mit den Gesetzen der Dualität in der projektiven Modelle können eine Reihe von Eigenschaften und Dual-Sätze aus der anderen zuvor abgezogen bekommen. Beziehen homologen Elemente in der projektiven Fallserie wurde durch den Erwerb Zwischen pespectividades erlaubt perspektivisch durchgeführt haben wir bekommen, was wir genannt haben “projektive Achse”. Wir werden, dass im Fall der projektiven Bündeln sehen, Dual-Argumentation führt uns zu projektiven Zentren bestimmen.
Die “Welt” Punkte ist günstiger als didaktisch gerade Dual, so haben wir die Analyse mit den Konzepten mit geradlinigen Reihe für zugehörige gestartet, jetzt, eine Entwicklung durchzuführen in der dualen Formen, gerade Balken.
Wir können in dieser Studie betrachten eine Reihe von grundlegenden Fragen, die helfen, die Entwicklung wird:
- Wie definieren wir zwei projektive?
- Wie viele homologen Elemente sind notwendig, um eine Projektivität bestimmen
- Wie können wir erhalten homologe Elemente aus gegebenen?
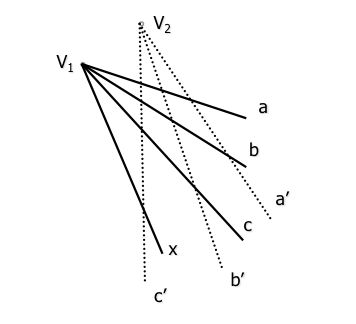
Zwei projektive Bündel sind entschlossen, drei Paare von homologen gerade definieren (a-a ', b-b ', c-c '), an ihren jeweiligen Basen liegt (Ursprung in ihren jeweiligen Ecken).
Ein viertes Element Strahl Ecke x “V1” wird ein neuer ray x haben’ Homolog Strahl (projektive) de base (Vertex) “V1”” so dass das Verhältnis der Quer Quaternionen wird die Bestimmung beibehalten:
(abcx) = (a'b'c'x ')
Um das Homolog von x bestimmen arbeiten mit Zwischen zwischen den Sätzen, die perspectividades beziehen (Schnitt) Elemente beider Strahlen.
 Durch das Studium der Perspektivität Wir sahen, dass Reihe von Perspektiven (Perspektive Zentrum mit einem gemeinsamen Scheitelpunkt hazproyección), mit einem Doppelpunkt, der in der Basis enthalten ist, (Schnittpunkt der Geraden Klammern) Serie.
Durch das Studium der Perspektivität Wir sahen, dass Reihe von Perspektiven (Perspektive Zentrum mit einem gemeinsamen Scheitelpunkt hazproyección), mit einem Doppelpunkt, der in der Basis enthalten ist, (Schnittpunkt der Geraden Klammern) Serie.
In der Figur ist der Doppelpunkt ist D = D’ enthält einen geraden R und R’ Reihe von perspektivischen perspektivischen Mittelpunkt mit V.
Diese Eigenschaft ist wichtig für die Suche nach Perspektiven Serie, die die beiden projektiven Bündel, die vereinfachte Behandlung bedeutet,, wie unten diskutiert.
Wenn zwei projektive Bündel frei V1 und V2, gehen, um sie durch zwei Linien r und r geschnitten’ Bestimmen Serie mit den Perspektiven, die tun. Unter den unzähligen Paaren von Linien, die wir verwenden können, um diese Strahlen zu trennen, wählen zwei durch irgendeinen Schnittpunkt der beiden homologen Elemente der Strahlen. Der Punkt D = D’ das Paar enthält d-d’ dieser Strahlen.
Estas series de puntos de bases r und r 'perspektivischen wobei jeder Doppelpunkt D = D '
Punkt Cp es el centro perspectivo de las series de Basen r und r ' dieser Abschnitt der Strahlstrahlen. Variieren einer der Basen der Reihe (r o r ') auf Schnitt D-D ', Diese Serie wird weiterhin Aussichten (mit einem Doppelpunkt) aber die Perspektive ändert sich von Mittelposition. Obwohl das Zentrum Änderungs, Aufbau zur Bestimmung der homologen Elemente bleiben gleich gültig.
Projektive Zentrum
Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“
El punto Cp es el centro perspectivo de las series de bases r y r’, wobei wiederum die centro proyectivo de los haces de Basen V1 y V2
Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.
Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.
Geometría Proyectiva





Muss sein in Verbindung gebracht einen Kommentar posten.