 The study of conic can be made from different geometric approaches. Uno de las análisis más usado es el que las determina a partir de secciones planas en un cono de revolución.
The study of conic can be made from different geometric approaches. Uno de las análisis más usado es el que las determina a partir de secciones planas en un cono de revolución.
From this definition it is possible to infer metric properties of these curves, plus new definitions of the same.
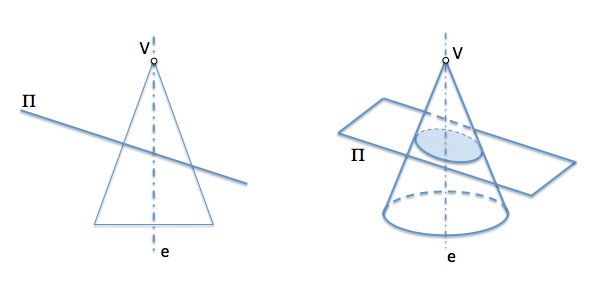
Utilizaremos para el análisis el caso en el que la curva resultado de la sección plana en un cono de revolución es una elipse. En este caso el ángulo que formaba el plano de la sección con el eje del cono era mayor que el semiángulo en el vértice.
Posteriormente se podrá analizar de forma similar los casos en los que la curva sea una parábola o una hipérbola.
Sea por lo tanto un cono de revolución de vértice “V..” y eje “and”, que se ha seccionado por un plano que no pase por su vértice. Este plano determina una curva que supondremos es una elipse para nuestro estudio.
Si consideramos una esfera tangente al plano y, simultaneously, a la superficie cónica, con su centro por lo tanto en el eje de esta forma geométrica. Esta esfera tendrá en contacto con el cono una circunferencia “c” contenida en un plano perpendicular a su eje “and”. La intersección de este plano con el que produce la sección es una recta que denominaremos directriz “d” de la cónica.
Al punto de contacto entre la esfera y el plano que contiene a la curva le denominaremos “Foco de la cónica”.
Al punto de la cónica que se encuentra en el plano de simetría del conjunto le denominaremos “Vértice de la cónica”
En el caso de la elipse podemos determinar una segunda esfera, por lo que esta curva tendrá dos vértices, dos focos y dos directrices.
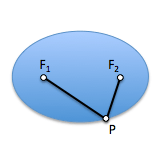
Si consideramos un punto “P” cualquiera de la curva y las distancias desde este punto a los focos de la elipse, PF1 and PF2, podemos determinar una propiedad métrica de esta curva que nos dará paso a una definición muy útil de la misma.
Como las tangentes desde un punto P a una esfera tienen igual longitud, se cumplirá que las tangentes desde P a la primera esfera, PF1 y PM, miden lo mismo. De igual forma ocurrirá con las tangentes desde este punto a la segunda esfera, PF2 y PN.
Por ello podemos determinar que la suma de estas dos distancias, PF1 y PF2, es igual a la distancia MN sobre la generatriz del cono limitada por los planos que contienen a las circunferencias de contacto c1 y c2.
This allows us to give a definition of the ellipse like the following:
Ellipse is the locus of points in a plane whose sum of distances from two fixed points, called Spotlights, It has a constant value.
If we consider the vertices of the conic as points of this locus, it is easy to show that the distance from one focus to one vertex is equal to the distance from the other focus to the other vertex and, with that, Show that the sum of the distances from a point of the ellipse to the foci is equal to the distance between the vertices of the conic.






Must be connected to post a comment.