En utilisant les lois de la dualité dans les modèles projectifs peut obtenir un ensemble de propriétés et de deux théorèmes de l'autre antérieurement déduits. Obtenir des éléments homologues dans la série de cas projective a été réalisée par l'obtention pespectividades intermédiaires perspectiviste permis ne nous obtenons ce que nous avons appelé “axe projectifs”. Nous allons voir que dans le cas de faisceaux projectifs, Double raisonnement nous conduit à déterminer les centres de projectifs.
Le “monde” points est plus abordable que didactique droite double, de sorte que nous avons commencé l'analyse avec les concepts associés à la série rectiligne pour, maintenant, réaliser le développement dans deux formes, poutres droites.
Nous pouvons considérer dans cette étude une série de questions de base qui aideront à guider le développement:
- Comment définissons-nous deux projective?
- Combien d'éléments homologues sont nécessaires pour déterminer un projectivit
- Comment pouvons-nous obtenir des éléments homologues de donnée?
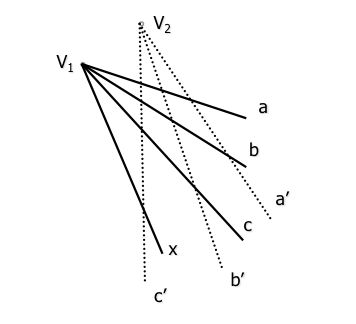
Deux faisceaux projectifs sont déterminés à définir trois paires de droite homologue (a-a ', b-b ', c-c '), situé sur leurs bases respectives (originaires de leurs sommets respectifs).
Un quatrième élément sommet de faisceau x “V1” dispose d'une nouvelle rayons x’ faisceau homologue (projective) de la base (sommet) “V1”” de sorte que le rapport transversale de quaternions est retenu détermination:
(abcx) = (a'b'c'x ')
Pour déterminer l'homologue de x fonctionne en utilisant l'intermédiaire entre les séries qui se rapportent perspectividades (coupe) des éléments des deux poutres.
En étudiant l' perspectivité nous avons vu que la série de points de vue (centre de perspective avec un hazproyección de sommet commun), avoir un point double qui est contenue dans la base (point d'intersection des droites supports) série.
Dans la figure, le point double est D = D’ contenant une droite r et r’ série de perspectiviste point central de perspective avec V.
Cette propriété est essentielle pour trouver des perspectives série reliant les deux faisceaux projectifs qui signifie traitement simplifié, comme on le verra ci-dessous.
Dados dos haces proyectivos de bases V1 y V2, procéder à leur couper par deux lignes r et r’ déterminer série avec les prospects qui font. Parmi les innombrables paires de lignes que nous pouvons utiliser pour couper ces poutres, choisir deux passant par un point d'intersection de deux éléments homologues des poutres. Le point D = D’ contient la paire d-d’ de ces poutres.
Estas series de puntos de bases r et r 'sont perspectif chaque point double étant D = D '
Point d' Cp es el centro perspectivo de las series de bases r y r ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, construction pour la détermination des éléments homologues restent également valables.
Centro proyectivo
Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“
El punto Cp es el centro perspectivo de las series de bases r y r’, étant à son tour l' centro proyectivo de los haces de bases V1 y V2
Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.
Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.
La géométrie projective
Doit être lié poster un commentaire.