One recommendation I always do my students is to try to solve the same problem in different ways, instead of many times the same problems with almost similar statements.

In one of my last classes we propose are obtaining the inverse of a point, an investment in the center and power is known. The proposed statement was as follows:

Since the square in Figure, in which one vertex is the center of inversion and the opposite vertex is a double point, determining the inverse of the point A (adjacent vertex).

Podemos buscar diferentes construcciones que se basen en los conceptos utilizados tanto en la metric geometry as in the projective geometry. Iniciaremos el estudio inicialmente con cinco soluciones de naturaleza métrica.

Investment in the plane

Empezaremos por recordar la relación métrica entre dos puntos inversos, estudiada en el capítulo de “Investment in the plane“.

1. La inversión es una transformación con centro. Cada punto A y su transformado A’ están alineados con el centro de inversión I.
2. El producto de distancias del centro de inversión a un punto y a su transformado es constante y se denomina potencia de inversión. IA*IA’=cte.

En el ejercicio propuesto, al conocerse un punto doble, conocemos la potencia de inversión que es el valor de la diagonal al cuadrado. Todos los puntos de una circunferencia de centro el de inversión y de radio la raíz de la potencia (diagonal del cuadrado) serán puntos dobles. Esta circunferencia se conoce como “circumference autoinversión”

1 Theorem catheter

El primer modelo propuesto se basaba en uno de los teoremas más usados en Metric Geometry, the “Teorema del Cateto”.

The Theorem catheter nos permite relacionar mediante una media proporcional el cateto de un triángulo rectángulo con su proyección sobre la hipotenusa y el producto con ella.

Theorem catheter

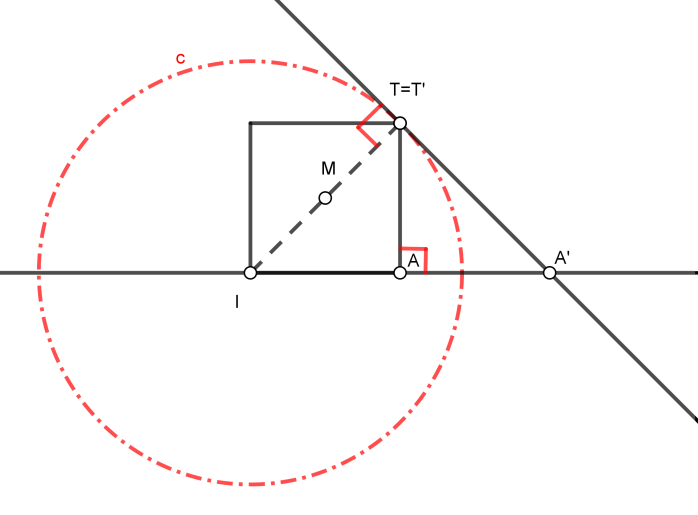
Si se considera al segmento IT como cateto de un triángulo rectángulo y al segmento IA como proyección de este cateto, al obtener la perpendicular por T se obtiene el punto A’ siendo IA’ la hipotenusa de un triángulo rectángulo.

2 Theorem catheter

A partir de este mismo concepto podemos realizar una nueva construcción en la que determinemos el arco capaz de 90º que va a soportar al triángulo rectángulo. Este arco capaz sobre el segmento buscado IA’ lo obtendremos ya que es una semicircunferencia que pasa por los puntos I and T, y tiene su centro en la recta IA. Determinaremos la mediatriz del segmento IT (que pasará por el punto A en este caso particular al ser la diagonal de un cuadrado) y de terminaremos el centro del arco capaz sobre la recta IA.

3 Power Concepts

The power of a point on a circle, que definimos como la mayor por la menor distancia del punto a dicha circunferencia y que es igual al segmento de tangencia (desde el punto a la circunferencia) squared, nos permite obtener nuevas construcciones.

En la figura vemos cómo el segmento de tangencia “the” es media proporcional entre “m” and “n”.

Para la nueva construcción determinaremos una circunferencia en la que IT es el segmento de tangencia y debe pasar además por el punto “A“, por lo que su centro estará en la intersección de la recta perpendicular a “I-T” by “T“, con la mediatriz de “A-T”

4 Power Concepts: Antiparallelism

The power concept of a point of a circumference product is based on the most for the least of the distances of a point to a circle.

These distance values ​​are given in the string that contains the center of the circle and the point, namely, in diameter containing said point. Es posible generalizar este concepto para considerar otras cuerdas que pasen por el punto P, como hemos visto en la “Generalización del concepto de potencia“.

Applying Thales theorem a los dos triángulos semejantes (PAD y PCB ya que comparten el ángulo en P y por ángulos en la circunferencia, arc able, son iguales en B y D) obteníamos que:

PA / PD = PC / PB

and therefore

PA * PB = PC * PD = Constant

Lo que demostraba que Power from the point P is independent of the chosen line, as we wanted to prove.

Las rectas AB y CD son antiparalelas de AD y CB formando dos a dos los mismos ángulos.

En nuestro caso la recta I-T-T’ y la I-A-A’ serán antiparalelas de A-T’ y A’-T, siendo en este caso un ángulo recto el que forman dos a dos.

5 Investment of a line

Al invertir figuras hemos visto que la inversa de una recta que no pasa por el centro de inversión es una circunferencia que si pasa por este punto, cuyo centro se encuentra en la perpendicular a la recta desde el centro de inversión.

La inversa del segmento A-T será un arco de circunferencia cuyo centro se situará sobre la recta I-A, y pasará por el centro de inversión “I” así como por el punto doble “T-T‘”

The 5 primeras soluciones son de naturaleza métrica. Veremos otras 5 utilizando los conceptos de la geometría proyectiva en el siguiente enlace.

(próximamente en este enlace ….) Solución proyectiva de la obtención del inverso de un punto

Metric geometry