Geometria projetiva: Centro projetivo de dois feixes projetivas

Usando as leis da dualidade em modelos projetivos pode obter um conjunto de propriedades e teoremas dupla de outros anteriormente deduzidos. Obtenção de elementos homólogos da série caso projetiva foi realizada mediante a obtenção de pespectividades intermediários autorizados perspectival obtemos o que chamamos “eixo projetivas”. Veremos que, no caso de pacotes projetivas, Raciocínio dupla nos leva a determinar centros projetivos.

O “mundo” pontos é mais acessível do que didaticamente reta dupla, então nós começamos a análise com os conceitos associados com a série retilíneo para, agora, realizar o desenvolvimento de formas duais, vigas retas.

Podemos considerar neste estudo uma série de perguntas básicas que vão ajudar a orientar o desenvolvimento:

• Como podemos definir dois projetiva?
• Quantos são necessários elementos homólogos para determinar uma projetividade
• Como podemos obter elementos homólogos de dado?

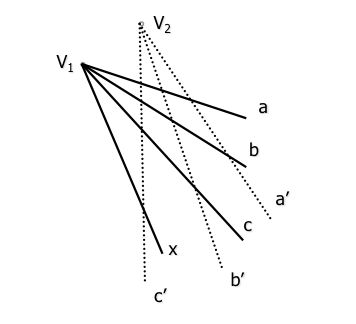
Dois feixes projetivas está determinado a definir três pares de reta homólogo (a-a ', b-b ', c-c '), localizados nas suas respectivas bases (originários de seus respectivos vértices).

Um quarto elemento feixe vértice x “V1” terá direito a um novo raio x’ feixe homólogo (projetiva) de base (vértice) “V1”” de modo que a razão transversal de cuaterniones é mantida a determinação:

(abcx) = (a'b'c'x ')

Para determinar o homólogo de x vai operar utilizando o intermediário entre conjuntos que se relacionam perspectividades (seccionado) elementos de ambos os feixes.

Ao estudar o perspectivity vimos que os séries perspectivas (centro perspectiva com um vértice comum hazproyección), tem um duplo ponto que está contido na base (intersecção das retas suportes) série.

Na figura o ponto duplo é D = D’ contendo uma r reta e r’ série de perspectival ponto central perspectivo com V.

Esta propriedade é essencial para encontrar séries perspectivas que liga os dois feixes projetivas que significa tratamento simplificado, como veremos a seguir.

Dados dos haces proyectivos de bases V1 e V2, proceder para cortá-los por duas linhas r e r’ determinar série com essas perspectivas que estão fazendo. Entre os inúmeros pares de linhas que podemos usar para cortar esses feixes, escolher dois passagem através de qualquer ponto de intersecção de dois elementos homólogos das vigas. O ponto D = D’ contém o par d-d’ Estes feixes.

Estas series de puntos de bases r e r 'são perspectivo sendo cada ponto de duplo D = D '

Ponto Cp es el centro perspectivo de las series bases de r e r ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, construção para a determinação de elementos homólogos permanecem igualmente válidas.

Projetiva Centro

Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“

El punto Cp es el centro perspectivo de las series de bases r y r’, sendo por sua vez o centro proyectivo de los haces bases de V1 y V2

Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.

Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.

Geometria projetiva