Una raccomandazione che faccio sempre i miei studenti è quello di cercare di risolvere lo stesso problema in modi diversi, invece di molte volte gli stessi problemi con dichiarazioni quasi simile.

In uno dei miei ultimi corsi che proponiamo sono ottenendo l'inverso di un punto, un investimento per il centro e la potenza è noto. La formulazione proposta è la seguente:

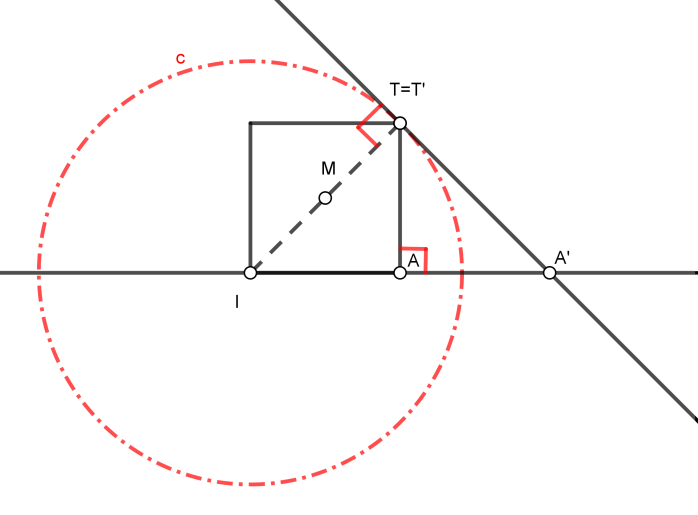
Poiché il quadrato di figura, in cui un vertice è il centro di inversione e il vertice opposto è un doppio punto, determinare l'inverso del punto A (vertice adiacente).

Podemos buscar diferentes construcciones que se basen en los conceptos utilizados tanto en la geometria metrica come nella geometria proiettiva. Iniciaremos el estudio inicialmente con cinco soluciones de naturaleza métrica.

Investimenti nel piano

Empezaremos por recordar la relación métrica entre dos puntos inversos, estudiada en el capítulo de “Investimenti nel piano“.

1. La inversión es una transformación con centro. Cada punto A y su transformado A’ están alineados con el centro de inversión I.
2. El producto de distancias del centro de inversión a un punto y a su transformado es constante y se denomina potencia de inversión. IA*IA’=cte.

En el ejercicio propuesto, al conocerse un punto doble, conocemos la potencia de inversión que es el valor de la diagonal al cuadrado. Todos los puntos de una circunferencia de centro el de inversión y de radio la raíz de la potencia (diagonal del cuadrado) serán puntos dobles. Esta circunferencia se conoce como “circonferenza autoinversión”

1 Teorema del catetere

El primer modelo propuesto se basaba en uno de los teoremas más usados en Geometria metrica, gli “Teorema del Cateto”.

Gli Catetere Teorema nos permite relacionar mediante una media proporcional el cateto de un triángulo rectángulo con su proyección sobre la hipotenusa y el producto con ella.

Teorema del catetere

Si se considera al segmento IT como cateto de un triángulo rectángulo y al segmento IA como proyección de este cateto, al obtener la perpendicular por T se obtiene el punto A’ siendo IA’ la hipotenusa de un triángulo rectángulo.

2 Teorema del catetere

A partir de este mismo concepto podemos realizar una nueva construcción en la que determinemos el arco capaz de 90º que va a soportar al triángulo rectángulo. Este arco capaz sobre el segmento buscado IA’ lo obtendremos ya que es una semicircunferencia que pasa por los puntos I e T, y tiene su centro en la recta IA. Determinaremos la mediatriz del segmento IT (que pasará por el punto A en este caso particular al ser la diagonal de un cuadrado) y de terminaremos el centro del arco capaz sobre la recta IA.

3 Concetti di potenza

Gli potencia de un punto respecto de una circunferencia, que definimos como la mayor por la menor distancia del punto a dicha circunferencia y que es igual al segmento de tangencia (desde el punto a la circunferencia) quadrato, nos permite obtener nuevas construcciones.

En la figura vemos cómo el segmento de tangencia “gli” es media proporcional entre “m” e “n”.

Para la nueva construcción determinaremos una circunferencia en la que IT es el segmento de tangencia y debe pasar además por el punto “A“, por lo que su centro estará en la intersección de la recta perpendicular a “I-T” da “T“, con la mediatriz de “A-T”

4 Concetti di potenza: Antiparallelismo

Gli concetto di potenza di un punto su un cerchio Si basa sul prodotto di vendita al dettaglio più grande le Distanze da un punto ad un cerchio.

Estos valores de la distancia se dan en la cuerda que contiene al centro de la circunferencia y al punto, vale a dire, di diametro che contiene quel punto. Es posible generalizar este concepto para considerar otras cuerdas que pasen por el punto P, como hemos visto en la “Generalización del concepto de potencia“.

Applicazione Teorema di Talete a los dos triángulos semejantes (PAD y PCB ya que comparten el ángulo en P y por ángulos en la circunferencia, arco in grado, son iguales en B y D) obteníamos que:

PA/PD = PC/PB

e quindi

PA * PB = PC * PD = costante

Lo que demostraba que la potenza dal punto P è indipendente del scelto dritto, come abbiamo voluto mostrare.

Las rectas AB y CD son antiparalelas de AD y CB formando dos a dos los mismos ángulos.

En nuestro caso la recta I-T-T’ y la I-A-A’ serán antiparalelas de A-T’ y A’-T, siendo en este caso un ángulo recto el que forman dos a dos.

5 Investimento di una linea

Al invertir figuras hemos visto que la inversa de una recta que no pasa por el centro de inversión es una circunferencia que si pasa por este punto, cuyo centro se encuentra en la perpendicular a la recta desde el centro de inversión.

La inversa del segmento A-T será un arco de circunferencia cuyo centro se situará sobre la recta I-A, y pasará por el centro de inversión “I” así como por el punto doble “T-T'”

Gli 5 primeras soluciones son de naturaleza métrica. Veremos otras 5 utilizando los conceptos de la geometría proyectiva en el siguiente enlace.

(próximamente en este enlace ….) Solución proyectiva de la obtención del inverso de un punto

Geometria metrica