軌跡センター円周接線として円錐

私たちは、円錐の研究は、異なる幾何学的なアプローチから作ることができることを見てきました.

特に, al iniciar el análisis de las cónicas hemos definido la elipse como lugar geométrico, 私たちは、と言いました:

楕円は、2 つの固定点までの距離の合計が平面上の点の幾何学的軌跡です。, フォーカスと呼ばれる, 一定の値がある.

この重要な曲線のこの計量定義により、接円の曲線と関連付けることによってその研究に取り組むことができます。, として知られている “アポロニウスの問題” 一部のバージョンでは. 放物線や双曲線の研究に取り組むときは、これらの概念を一般化して問題を次の点に還元するために問題を再説明します。 “直線の場合の接線の基本的な問題“, o el “円周の場合の接線の基本的な問題“, すなわち, の円周を決定する “ハズ・コーラディカル” 接線条件付き.

Supongamos, aplicando la definición anterior de la elipse, que los puntos fijos son F1 Y F2. Estos puntos son los focos de la elipse. Supongamos además que la cónica se termina de definir por la condición de paso por un punto dado P.

Según la definición anterior la suma de distancias desde P a los dos focos debe ser constante. Llamaremos a esa suma “2へ”.

ρ1 + ρ2 = 2a = constante

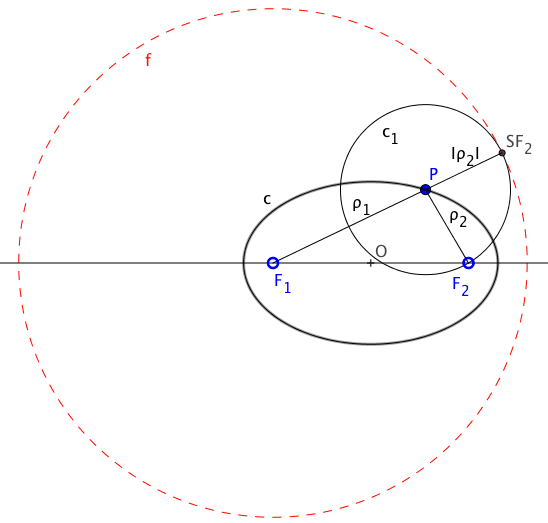
Si llevamos el segmento ρ2 a continuación del punto P según la dirección del segmento ρ1, obtendremos un punto “SF2” que dista del foco F1 el valor “2へ“.

Al obtener todos los puntos de la cónica, como la suma de distancias a los focos es “2へ“, los puntos similares al “SF2” se encontrarán a esa distancia (2へ) del foco F1, por lo que se encontrarán en una circunferencia denominada “Circunferencia focal de la elipse“.

La circunferencia focal de una cónica es aquella circunferencia que tiene su centro en uno de sus focos y su radio es igual a la distancia entre los vértices de la cónica (2へ)

Como la distancia del punto P al foco F2 que no es centro de la focal, es la misma que al punto “SF2”, la circunferencia que tiene su centro en el punto P y radio el valor “ρ2” を通過します。 “SF2” punto de la circunferencia focal, pero como además los centros “F1” de la focal y “P” de esta nueva circunferencia se encuentran alineados con el punto común de ambas “SF2”, este punto es de tangencia entre las dos circunferencias, lo que nos permite concluir que:

Los puntos de una elipse son los centros de las circunferencias que siendo tangentes a la circunferencia focal, pasan por el otro foco.

Esta definición de la cónica nos permite abordar los problemas de determinación de tangentes y puntos de paso o tangencia a la cónica mediante la solución de problemas de tangencias.

例えば, determinar los puntos de intersección de una recta con una cónica es determinar las circunferencias que tienen su centro sobre la recta, pasan por un foco y son tangentes a la circunferencia focal. Al tener su centro sobre la recta y pasar por un foco, pasarán por el simétrico de dicho foco respecto de la recta y el problema se reducirá a buscar circunferencias que pasando por dos puntos (foco y simétrico) son tangentes a la focal, すなわち, dos puntos de paso (pertenencia a un haz elíptico) y una condición de tangencia respecto de la circunferencia focal: 接線の根本的な問題.

Igual que obtenemos los puntos de una recta podemos relacionar las tangentes y los puntos de tangencia como se aprecia en la siguiente figura. Al ser la recta “R” tangente a la cónica, se puede deducir que es “la bisectriz” de los radios focales ρ1 Y ρ2, como veremos más adelante.

¿Serías capaz de deducirlo tú?

計量幾何学