Una recomendación que hago siempre a mis alumnos es que traten de resolver un mismo problema de formas diferentes, en lugar de hacer muchas veces los mismos problemas con enunciados casi similares.

En una de mis últimas clases planteamos la obtención del inverso de un punto, 中心部や電源への投資が知られています. 次のように提案した声明でした:

図中の四角以来, ここで一つの頂点を反転の中心であると反対の頂点が二重点であります, 点Aの逆を決定します (隣接する頂点).

Podemos buscar diferentes construcciones que se basen en los conceptos utilizados tanto en la 計量幾何学 ように、 射影幾何学. Iniciaremos el estudio inicialmente con cinco soluciones de naturaleza métrica.

平面への投資

Empezaremos por recordar la relación métrica entre dos puntos inversos, estudiada en el capítulo de “平面への投資“.

1. La inversión es una transformación con centro. Cada punto A y su transformado A’ están alineados con el centro de inversión 私.
2. El producto de distancias del centro de inversión a un punto y a su transformado es constante y se denomina potencia de inversión. IA*IA’=cte.

En el ejercicio propuesto, al conocerse un punto doble, conocemos la potencia de inversión que es el valor de la diagonal al cuadrado. Todos los puntos de una circunferencia de centro el de inversión y de radio la raíz de la potencia (diagonal del cuadrado) serán puntos dobles. Esta circunferencia se conoce como “周autoinversión”

1 定理カテーテル

El primer modelo propuesto se basaba en uno de los teoremas más usados en 計量幾何学, エル “Teorema del Cateto”.

ザ 定理カテーテル nos permite relacionar mediante una media proporcional el cateto de un triángulo rectángulo con su proyección sobre la hipotenusa y el producto con ella.

定理カテーテル

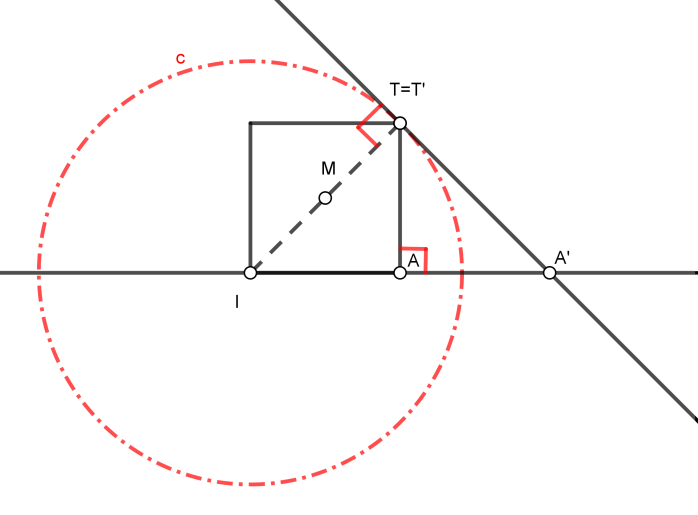
Si se considera al segmento IT como cateto de un triángulo rectángulo y al segmento IA como proyección de este cateto, al obtener la perpendicular por T se obtiene el punto A’ siendo IA’ la hipotenusa de un triángulo rectángulo.

2 定理カテーテル

A partir de este mismo concepto podemos realizar una nueva construcción en la que determinemos el arco capaz de 90º que va a soportar al triángulo rectángulo. Este arco capaz sobre el segmento buscado IA’ lo obtendremos ya que es una semicircunferencia que pasa por los puntos 私 Y T, y tiene su centro en la recta IA. Determinaremos la mediatriz del segmento IT (que pasará por el punto A en este caso particular al ser la diagonal de un cuadrado) y de terminaremos el centro del arco capaz sobre la recta IA.

3 パワーの概念

ザ 円を基準としてポイントの力, que definimos como la mayor por la menor distancia del punto a dicha circunferencia y que es igual al segmento de tangencia (desde el punto a la circunferencia) 自乗, nos permite obtener nuevas construcciones.

En la figura vemos cómo el segmento de tangencia “ザ” es media proporcional entre “M” Y “N”.

Para la nueva construcción determinaremos una circunferencia en la que IT es el segmento de tangencia y debe pasar además por el punto “A“, por lo que su centro estará en la intersección de la recta perpendicular a “I-T” によって “T“, con la mediatriz de “A-T”

4 パワーの概念: 反平行

ザ 円周の点の電力概念 製品は円にポイントの距離のうちの最もに基づいています.

これらの距離値は、円の中心と点を含む文字列で与えられ, すなわち, 直径含有する点は言った. Es posible generalizar este concepto para considerar otras cuerdas que pasen por el punto P, como hemos visto en la “Generalización del concepto de potencia“.

適用 タレスの定理 a los dos triángulos semejantes (PAD y PCB ya que comparten el ángulo en P y por ángulos en la circunferencia, できるアーク, son iguales en B y D) obteníamos que:

PA / PD = PC / PB

したがって

PA * PB = PC * PD =定数

Lo que demostraba que 点Pからの電力は、選択された行とは無関係です, 我々は証明したかったよう.

Las rectas AB y CD son antiparalelas de AD y CB formando dos a dos los mismos ángulos.

En nuestro caso la recta I-T-T’ y la I-A-A’ serán antiparalelas de A-T’ y A’-T, siendo en este caso un ángulo recto el que forman dos a dos.

5 ラインの投資

Al invertir figuras hemos visto que la inversa de una recta que no pasa por el centro de inversión es una circunferencia que si pasa por este punto, cuyo centro se encuentra en la perpendicular a la recta desde el centro de inversión.

La inversa del segmento A-T será un arco de circunferencia cuyo centro se situará sobre la recta I-A, y pasará por el centro de inversión “私” así como por el punto doble “T-T'”

ラス 5 primeras soluciones son de naturaleza métrica. Veremos otras 5 utilizando los conceptos de la geometría proyectiva en el siguiente enlace.

(próximamente en este enlace ….) Solución proyectiva de la obtención del inverso de un punto

計量幾何学