 The study of the disciplines of classical geometry can be reinforced by using tools that allow constructions that can be changed dynamically: variational constructions.
The study of the disciplines of classical geometry can be reinforced by using tools that allow constructions that can be changed dynamically: variational constructions.
These constructs can serve to understand how certain properties are maintained in geometric relationships that denominate “Invariant”, and to verify that certain concepts that we as axioms are simply valid under certain conditions. It also helps us understand how varies a representation by changing the arrangement of the elements involved in the same, facilitating the widespread and deep understanding of geometric principles.
The tool “Geogebra” It will serve to illustrate these concepts and demonstrate the importance of detailed knowledge of geometric relationships to ensure the robustness of the buildings we use in geometric reasoning, as, sometimes, some constructions may lose their validity.
Polar of a point of a circle.
See with a relatively simple example how the use of either construction can lead to situations where the most basic geometry longer application.
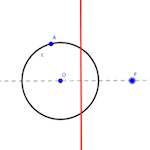
Suppose we have a circumference “c” center “O” que pasa por un determinado punto “A”, and a point “P” que en principio es exterior a esta circunferencia.
A partir de estos datos nos planteamos determinar una straight que sea la polar de P respecto de la circunferencia c.
¿Qué es la polar de un punto respecto de una circunferencia? La respuesta a esta pregunta nos puede conducir a una u otra construcción geométrica.
Es el lugar geométrico de los extremos de los diámetros de las circunferencias que pasando por el punto P son ortogonales a la circunferencia c.
Las circunferencias que pasan por un punto y son ortogonales a otra circunferencia se encuentran agrupadas en un beam circumferences. Si consideramos al punto como una circunferencia de radio nulo, los centros estarán en el eje radical de la circunferencia y el punto determinando un elliptical beam circumferences (conjugado del hyperbolic formado por la circunferencia c y el punto P)
Para determinar este lugar geométrico podemos obtener un punto de paso ya que sabemos que es una recta perpendicular al diámetro de la circunferencia c que con tiene al punto P (perpendicular a la recta O-P).
Mediante una recta tangente desde P a la circunferencia podemos obtener el punto T de tangencia por el que pasará la polar. La determinación de un arc able of 90 grados (ángulo recto) entre el punto P y el centro O nos permitirá obtener este punto T de tangencia por el que pasará la recta polar.
La circunferencia de diámetro PT es ortogonal a la circunferencia c ya que sus radios en el punto T de contacto son ortogonales por lo que T cumple con el lugar geométrico que hemos usado para definir la recta polar.
Sin embargo esta construcción tan sencilla pierde su validez en el momento en el que el punto P pasa a ser interior a la circunferencia c, como puede observarse en la siguiente figura, ya que el arco capaz no corta a la circunferencia c. Deberemos buscar nuevos modelos que resuelvan estas posiciones.
Es el lugar geométrico de los puntos conjugados de P respecto de la circunferencia c.
Recordaremos que una cuaterna de puntos (ABCD) cuyo valor es la unidad negativa se denomina cuaterna armónica, namely:
(ABCD)=-1
Being
(ABCD) = (ACD)/(BCD) = (AC/AD)/(BC/BD)
En su momento definíamos la polar de un punto P respecto de dos rectas a y b como el lugar geométrico de los conjugados del punto P respecto de los de intersección con “to” and “b” del haz de rectas con vértice en P.
A partir de la geometría del full cuadrivertice podíamos obtener la recta que cumplía las condiciones solicitadas, siendo (PP ’ AB)=-1.
Este modelo nos permite realizar una nueva construcción para determinar la polar respecto de la circunferencia mediante el cuadrivértice ABCD que se puede obtener con un diámetro de la circunferencia y la cuerda AD resultado de proyectar desde P el punto A que determina el radio de nuestra circunferencia. In this case:
(PP1AD)=(PP2BC)=-1
luego la recta que pasa por los puntos diagonales del cuadrivértice (D1 and D2) es el lugar geométrico buscado.
Al modificar la posición del punto P se conserva la robustez del modelo, en el que ademas no ha sido necesario utilizar ninguna circunferencia (solución lineal).
Existen otras soluciones que pueden ser híbridas entre las anteriores, en las que se pueden utilizar circunferencias auxiliares para determinar ejes radicales que impliquen la ortogonalidad, sabiendo que la recta O-P es además el eje radical del haz conjugado. Se deja al lector el análisis de esta nueva y simple construcción.
Modelo variacional con GeoGebra
Para terminar se añade el fichero Geogebra con la geometría dinámica que permitirá al lector experimentar variando las posiciones de los elementos.
¿Sabrías realizar una nueva construcción robusta que permitiera variar las posiciones de los elementos sin perder su validez?











Must be connected to post a comment.