Conical defined by the two foci and a tangent

Hemos resuelto la determinación de una cónica definida por sus dos focos y un punto mediante la circunferencia focal de la cónica.

A problem using identical concepts is determining a known conic its foci and their tangents. We will see this problem in the case of an ellipse.

Supongamos que los datos son los focos de una elipse, F1 and F2, y una cualquiera de sus tangentes, t in Figure.

El simétrico de uno de los focos respecto de la tangente debe encontrarse sobre la circunferencia focal de centro el otro foco.

Como la tangente es bisectriz de los radios focales, podemos determinar el punto de tangencia

Para determinar los vértices podemos apoyarnos en el valor del radio de la circunferencia focal, 2to, ya que es la suma, constant, de los dos radios focales de cada punto de la cónica, tal y como vimos en la definición como lugar geométrico de circunferencias tangentes a la focal que pasaban por un punto dado.

Definition of the conical locus as centers of circumferences

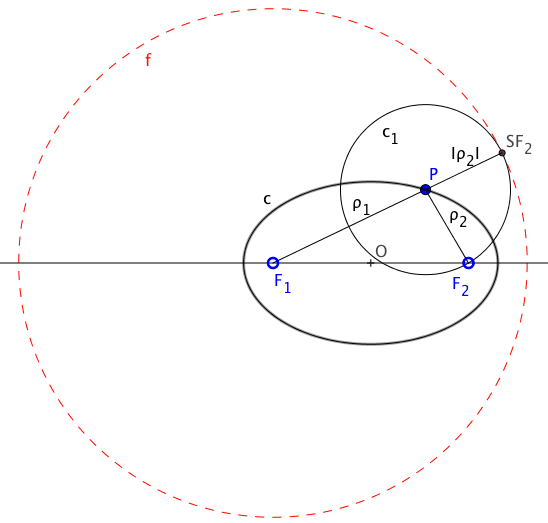
In this case if the point of tangency step is T, The distance of this point the focus is no focal center (F2) It is the same as the distance to the focal circumference (SF2). The point T will be in the radius of the focal circle through the other focus symmetric with respect to the tangent.

Taper is defined by the main elements when the foci are known and vertices.

What if instead of one focus we had two tangents more? Can you find the other focus?

The problem would determine the cone which is defined by a center and three tangents.

GEOMETRÍA MÉTRICA