射影幾何: 2射影バンドルの射影センター

射影モデルで二重性の法則を使用すると、他の以前に控除からプロパティとデュアル定理のセットを取得することができます. 遠近許さ中間pespectividadesを取得することによって実行された射影ケースシリーズ中の相同の要素を取得する我々は我々が求めているものを手に入れるか “射影軸”. 私たちは、射影バンドルの場合とが表示されます, デュアル推論は射影センターを決定するために私たちをリード.

ザ “世界” ポイントは教訓的にストレートデュアルよりも手頃な価格です, 従って私達はのための直線のシリーズに関連する概念と分析を開始している, 今, デュアル形で開発を行う, ストレートビーム.

我々は、この研究で開発を導く手助けとなる基本的な一連の質問を考慮することができる:

• どのように我々は2射影を定義します?
• 相同要素はprojectivityを決定する必要がいくつあるか
• どのように我々は与えられたから、相同要素を得ることができます?

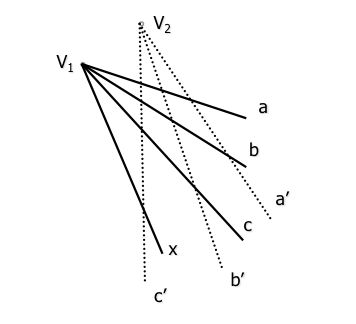
二つの射影束は相同直三対を定義するために決定される (-A ', のB-B ', C-C '), それぞれの拠点に配置され (それぞれの頂点に起因).

第4の素子ビーム頂点X “V1” 1新線Xをもたなければならない’ ホモログビーム (射影の) ベース (頂点) “V1”” 四元数の断面比を決定保持されるように、:

(ABCX) = (a'b'c'x ')

Xのホモログを決定するためにperspectividadesを関連付けるセット間の中間を使用して動作します (区分された) 両ビームの要素.

勉強することで 配景 我々は視点のシリーズを見た (共通の頂点hazproyecciónと投影中心), ベースに含まれている二重のポイントを持っている (ストレートブラケットの交差点) シリーズ.

図では二重のポイントは、D = Dである’ ストレート、RおよびRを含む’ Vとの遠近遠近中心点のシリーズ.

このプロパティは、単純化された処理を意味する2射影バンドルを結ぶ見通しシリーズを見つけるために不可欠である, 以下に説明するように.

Dados dos haces proyectivos de bases V1 Y V2, 2行RとRによってそれらを切るに進み’ やっているものの見通しと直列を決定. 我々はこれらのビームを切断するために使用できるラインの無数のペアのうち、, ビームの2相同要素の交点の任意のポイントを介して2つの通過を選択する. 点D = D’ ペアが含まれています d-d’ これらのビームの.

Estas series de puntos de bases RおよびR 'は遠近です それぞれが二重点、D = D '

ポイント Cp es el centro perspectivo de las series デ·拠点 R Y R ' que seccionan los rayos de los haces. Al variar cualquiera de las bases de las series (r o r’) sobre el punto D-D’, estas series seguiran siendo perspectivas (al tener un punto doble) pero el centro perspectivo cambiará de posición. Aunque el centro cambie, 相同要素を決定するための工事が等しく有効なまま.

射影センター

Al usar dos rayos homólogos como bases de las series r y r’, estas son perspectivas al tener un elemento doble. Estamos en el caso anterior ya que las bases se encuentran pasando por un punto (D-D’) que contiene a dos elementos homólogos, pero en este caso el centro perspectivo de las series es único y no depende de la pareja de rayos elegidos para generar las series perspectivas. Si seccionamos por lo tanto desde a-a’ o b-b’ … el centro perspectivo es el mismo y lo llamaremos “centro proyectivo de los haces“

El punto Cp es el centro perspectivo de las series de bases r y r’, 今度はいる centro proyectivo de los haces デ·拠点 V1 y V2

Los rayos m=n’ de la proyección de las dos bases (rectas V1-V2) tienen por homólogos los de proyección desde el centro de las correspondientes bases.

Veremos más adelante cómo utilizar el centro proyectivo para determinar pares de elementos homólogos de los haces.

射影幾何